In This Topic
Mean (Normal)
Standard deviation is known
The confidence interval for a mean from a normal distribution when the population standard deviation is known is:

The margin of error is 
To solve for n:

Standard deviation is not known
The confidence interval for a mean from a normal distribution when the population standard deviation is unknown is:
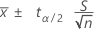
The margin of error is 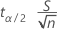
To solve for n, calculate the minimum n such that:
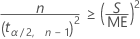
Notation
| Term | Description |
|---|---|
 | sample mean |
| zα/2 | inverse cumulative probability of the standard normal distribution at 1- α /2; α = 1 - confidence level/100 |
| σ | population standard deviation (assumed known) |
| n | sample size |
| ME | margin of error |
| t α/2 | inverse cumulative probability of a t distribution with n-1 degrees of freedom at 1-α/2 |
| S | planning value |
Proportion (Binomial)
Lower limit
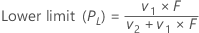
Upper limit
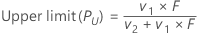
The interval (PL, PU) is an approximate 100(1 – α)% confidence interval of p.
Note
To solve for n, calculate the minimum n such that:
Notation
| Term | Description |
|---|---|
| v1 (lower limit) | 2x |
| v2 (lower limit) | 2(n – x + 1) |
| v1 (upper limit) | 2(x + 1) |
| v2 (upper limit) | 2(n – x) |
| x | number of events |
| n | number of trials |
| F (lower limit) | lower α/2 point of F distribution with v1 and v2 degrees of freedom |
| F (upper limit) | upper α/2 point of F distribution with v1 and v2 degrees of freedom |
Rate and Mean (Poisson)
Formula
The lower bound confidence limit for a rate or mean from a Poisson distribution is:
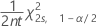
The upper bound confidence limit for a rate or mean from a Poisson distribution is:
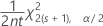
The lower margin of error equals −1 × (lower bound confidence limit). The upper margin of error equals the upper bound confidence limit.
To solve for n, calculate the minimum n such that:
(S – SL) ≤ ME and (SU – S) ≤ ME
Notation
| Term | Description |
|---|---|
| n | sample size |
| t | length of observation; for the Poisson mean, length = 1 |
| s | total number of occurrences in a Poisson process |
| χ2p, x | upper x percentile point of a chi-square distribution with p degrees of freedom, where 0 < x < 1 |
| S | planning value |
| ME | margin of error |
Variance and Standard Deviation (Normal)
Formula
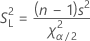
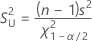
To obtain the confidence interval for the standard deviation, take the square root of the above equations.
The lower margin of error equals −1 × (lower bound confidence limit). The upper margin of error equals the upper bound confidence limit.
To solve for n for variance, calculate the minimum n such that:
(S2 – S2L) ≤ ME and (S2U – S2) ≤ ME
To solve for n for standard deviation, calculate the minimum n such that:
(S – SL) ≤ ME and (SU – S) ≤ ME
Notation
| Term | Description |
|---|---|
| n | sample size |
| s2 | sample variance |
| Χ2 p | upper 100pth percentile point on a chi-square distribution with (n – 1) degrees of freedom |
| S | planning value |
| ME | margin of error |
