Minitab calculates 3 types of residuals.
Regular residuals
A residual is the difference between an observed value (y) and its corresponding fitted value (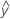 ).
).
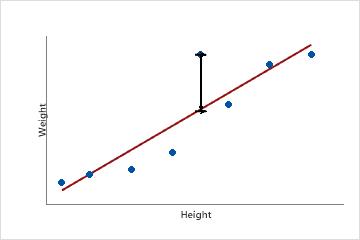
For example, this scatterplot plots people's weight against their height. The fitted regression line plots the fitted values of weight for each observed value of height. Suppose a person is 6 feet tall and the fitted value of their weight is 190 lbs. If their actual weight is 200, the residual is 10.
Plot the residuals, and use other diagnostic statistics, to determine whether your model is adequate and the assumptions of regression are met. The residuals can also identify how much a model explains the variation in the observed data.
Standardized residuals
The standardized residual equals the value of a residual, ei, divided by an estimate of its standard deviation. Standardized residuals greater than 2 and less than -2 are usually considered large and Minitab identifies these observations with an 'R' in the table of unusual observations and the table of fits and residuals. The observations that Minitab labels do not follow the proposed regression equation well. However, it is expected that you will have some unusual observations. For example, based on the criteria for large standardized residuals, you would expect roughly 5% of your observations to be flagged as having a large standardized residual.
Use the standardized residual to help you detect outliers. Standardizing residuals is useful because raw residuals might not be acceptable identifiers of outliers when they have nonconstant variance. If residuals with x-values farther from  have greater variance than residuals with x-values closer to
have greater variance than residuals with x-values closer to  then outliers are harder to detect. Standardizing controls for this nonconstant variance, and all standardized residuals have the same standard deviation.
then outliers are harder to detect. Standardizing controls for this nonconstant variance, and all standardized residuals have the same standard deviation.
Standardized residuals are also called internally Studentized residuals.
Studentized deleted residuals
The Studentized deleted residual of an observation is calculated by dividing an observation's deleted residual by an estimate of its standard deviation. A deleted residual di is the difference between yi and its fitted value in a model that omits the ith observation from its calculations. The observation is omitted to determine how the model behaves without this potential outlier. If an observation has a large Studentized deleted residual (if its absolute value is greater than 2), it may be an outlier in your data.
Use the deleted residual to help you detect outliers. Deleted residuals are useful because raw residuals might not be acceptable identifiers of outliers when they have nonconstant variance. If residuals with x-values farther from 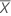 have greater variance than residuals with x-values closer to
have greater variance than residuals with x-values closer to 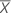 then outliers are harder to detect. All deleted residuals have the same standard deviation.
then outliers are harder to detect. All deleted residuals have the same standard deviation.
Each Studentized deleted residual follows the t distribution with (n – 1 – p) degrees of freedom, where p equals the number of terms in the regression model.
Studentized deleted residuals are also called externally Studentized residuals or deleted t residuals.
