Note
This command is available with the Predictive Analytics Module. Click here for more information about how to activate the module.
MARS® Regression essentially builds flexible models by fitting piecewise linear regressions. The model has the restriction that the endpoints of the piecewise lines join evenly. Approximations of the nonlinearity of the models use separate regression slopes in distinct intervals of the data. An approximation of the process is easy to visualize in the simple, 2-dimensional case.
In the 2-dimensional case, a single, straight line fits the data. This model provides a baseline for testing the improvement of adding additional complexity.
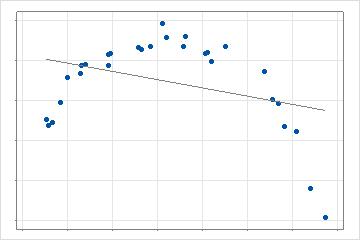
In the next step, the analysis searches for the value of a predictor that creates a basis function that leads to the greatest improvement in the search criterion. The calculation of the criterion depends on the selection for the analysis and on the validation method. In the 2-dimensional case, this model is a piecewise, linear regression with 2 lines instead of 1 line. With multiple predictors, the search for the best data point evaluates each predictor that the analysis permits.

After the analysis finds the first value that provides the best improvement, the analysis searches the remaining predictor values to find the best improvement over the current model. In the 2-dimensional case, this model has 3 lines that describe different portions of the data. The search repeats up to the maximum number of basis functions for the analysis. When interactions are allowed, the analysis performs additional series of searches by multiplying the candidate basis functions with other basis functions that are already present in the model.
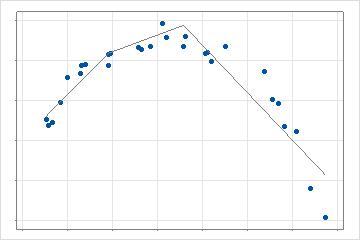
After the analysis rapidly fits the maximum number of basis functions and estimates the parameters of those functions, the analysis identifies the optimal number of basis functions. The optimal number of basis functions uses a stepwise, backwards elimination approach to find the number of basis functions with the best value of the optimality criterion.
Missing values for the model fit
In the search for the basis functions, MARS® Regression creates indicator variables for any predictors with missing values. The indicator variable shows whether a value of the predictor is missing. If the analysis includes a basis function for a predictor with missing values in the model, then the model also includes a basis function for the indicator variable. The other basis functions for the predictor all interact with the basis function for the indicator variable.
When a predictor has a missing value, the basis function for the indicator variable nullifies all the other basis functions for that predictor through multiplication by 0. These basis functions for missing values are in all models where important predictors have missing values, even additive models and models that disable other types of transformations.
Missing values for prediction
MARS® Regression calculates predictions when predictors in the model have missing values. The analysis uses different strategies depending on whether missing values for the predictor were present when the analysis fit the model. If missing values for the predictor were present when the analysis fit the model, then the basis functions in the model include an indicator variable that removes the predictor from the model when the predictor has a missing value.
The second case is when the values for prediction include missing values for a predictor but the predictor did not have missing values when the analysis fit the model. To calculate predictions in this case, the analysis imputes the missing value. For a continuous predictor, the mean of the predictor replaces the missing value. For a categorical predictor, the final non-missing value in the data set replaces the missing value.
