Exponential family and link functions
The extension of the classical linear models to generalized linear models has two parts: a distribution from the exponential family and a link function.
The exponential family
The first part extends the linear model to response variables that are members of a large family of distributions called the exponential family. Members of the exponential family of distributions have probability distribution functions for an observed response in this general form:
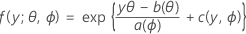
where a(∙), b(∙), and c(∙) depend on the distribution of the response variable. The parameter θ is a location parameter that is often called the canonical parameter, and ϕ is called the dispersion parameter. The function a(ϕ) is usually of the form a(ϕ)= ϕ/ ω, where ω is a known constant or weight that may vary from one observation to another. (In Minitab, when weights are given the function a(ϕ), is adjusted accordingly.)
Members of the exponential family can be discrete distributions or continuous distributions. Examples of continuous distributions that are members of the exponential family are the normal and the gamma distributions. Examples of discrete distributions that are members of the exponential family are the binomial and the Poisson distributions. The following table gives the characteristics of some of these distributions.
| Distribution | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| Normal | σ2 | θ2/2 | φω |  |
| Binomial | 1 | 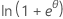 |
φ/ω | -ln(y!) |
| Poisson | 1 | exp(θ) | φ/ω |  |
The link function
The second part is the link function. The link function relates the mean of the response in the ith observation to a linear predictor in this form:
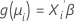
The classical linear model is a special case of this general formulation where the link function is the identity function.
The choice of the link function in the second part depends upon the specific distribution of the exponential family of the first part. In particular, each distribution in the exponential family has a special link function called the canonical link function. This link function satisfies the equation g (μi) = Xi'β= θ, where θ is the canonical parameter. The canonical link function results in some desirable statistical properties of the model. Goodness-of-fit statistics can be used to compare fits using different link functions. Certain link functions may be used for historical reasons or because they have a special meaning in a discipline. For example, an advantage of the logit link function is that it provides an estimate of the odds ratios. Another example is that the normit link function assumes that there is an underlying variable that follows a normal distribution that is classified into binary categories.
Minitab provides three link functions. The different link functions make it possible to find models that adequately fit a wider variety of data. The link functions are logit, normit (also called probit), and gompit (also called complementary log-log). These are the inverse of the standard cumulative logistic distribution function (logit), the inverse of the standard cumulative normal distribution function (normit), and the inverse of the Gompertz distribution function (gompit). The logit is the canonical link function for binomial models, thus the logit is the default link function.
| Model | Name | Link Function, g(μi) |
| Binomial | logit | 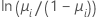 |
| Binomial | normit (probit) | 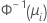 |
| Binomial | gompit (complementary log-log) |  |
Notation
| Term | Description |
|---|---|
| μi | the mean response of the ith row |
| g(μi) | the link function |
| X | the vector of predictor variables |
| β | the vector of coefficients associated with the predictors |
 | the inverse cumulative distribution function of the normal distribution |
Factor/covariate pattern
Describes a single set of factor/covariate values in a data set. Minitab calculates event probabilities, residuals, and other diagnostic measures for each factor/covariate pattern.
For example, if a data set includes the factors gender and race and the covariate age, the combination of these predictors may contain as many different covariate patterns as subjects. If a data set only includes the factors race and sex, each coded at two levels, there are only four possible factor/covariate patterns. If you enter your data as frequencies, or as successes, trials, or failures, each row contains one factor/covariate pattern.
Design matrix
First, Minitab creates a design matrix from the factors and the model that you specify. The columns of this matrix represent the terms in the model. Then, Minitab adds additional columns for the constant term, blocks, and higher-order terms to complete the design matrix for the model in the analysis.
Designs with all continuous factors
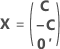
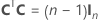
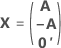
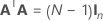
The full design matrix contains columns besides the columns that represent factors. The design matrix contains a column of 1s for the constant term. The full design matrix also includes columns that represent any square or interaction terms in the model.
Designs with categorical factors
For a design that includes categorical factors, Minitab replaces the single center point row in the design matrix with 2 pseudo center points. If the design has only 1 categorical factor, only two possible pseudo center points exist, so both points are in the design.
In the case where the design has more than 2 categorical factors, Minitab uses an iterative algorithm to select 2 pseudo center points to include. The algorithm seeks to minimize the variance of the regression coefficients for the linear effects in the model.
Notation
| Term | Description |
|---|---|
| C | A conference matrix |
| 0' | A row of zeroes in a matrix that represent a center point run |
| In | the n × n identity matrix |
| A | A matrix that is a subset of a conference matrix with N rows and n columns where  |
| N | The number of rows in the subset of the columns from the conference matrix |
| n | The number of factors in a design |
