Method for controlling the simultaneous confidence level for an entire set of confidence intervals. It is important to consider the simultaneous confidence level when you examine multiple confidence intervals because your chances that at least one of the confidence intervals does not contain the population parameter is greater for a set of intervals than for any single interval. To counter this higher error rate, the Bonferroni method adjusts the confidence level for each individual interval so that the resulting simultaneous confidence level is equal to the value you specify.
Example of Bonferroni confidence intervals
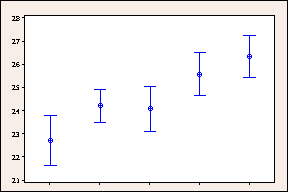
Unadjusted 95% Confidence Intervals for Delivery Times by Shipping Center
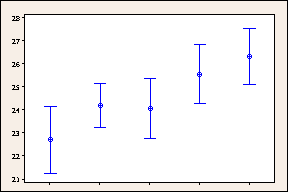
Bonferroni 95% Confidence Intervals for Delivery Times by Shipping Center (99% Individual Confidence Intervals)
These graphs compare regular 95% confidence intervals to the Bonferroni 95% confidence intervals. The wider Bonferroni confidence intervals provide less precise estimates of the population parameter but limits the probability that one or more of the confidence intervals does not contain the parameter to a maximum of 5%. In comparison, the family error rate associated with the five regular 95% confidence intervals is 25%.
This conservative method ensures that the overall confidence level is at least 1 - α. To obtain an overall confidence level of 1 - α for the joint interval estimates, Minitab constructs each interval with a confidence level of (1 - α/g), where g is the number of intervals. In the Bonferroni intervals, Minitab uses 99% confidence intervals (1.00 - 0.05/5 = 0.99) to achieve the 95% simultaneous confidence level.
