In This Topic
Conditional fitted value
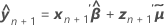
Notation
| Term | Description |
|---|---|
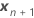 | the vector of the new settings for the fixed effect terms |
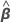 | the estimated coefficients for the fixed effect terms |
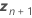 | The vector of the new settings for the random terms |
 | he BLUP predictions for the random terms |
Standard error of the conditional fitted value (SE Fit)
The standard error of a conditional fitted value equals the square root of the following variance expression.
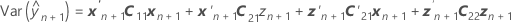
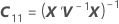
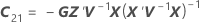

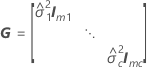
X is the design matrix for the fixed effect terms and Z is the design matrix for the random terms.
Confidence intervals for conditional means
The range in which the mean response for a given set of predictor values is expected to fall.

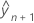 is the conditional fit.
is the conditional fit. 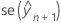 is the standard error of he fit.
is the standard error of he fit.
The degrees of freedom use this formula for the conditional case:
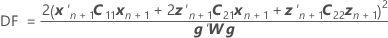
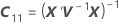
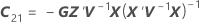

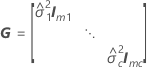
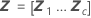
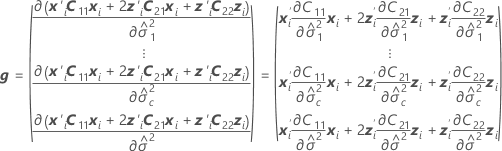



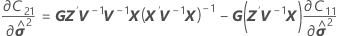
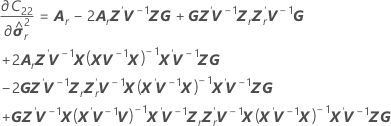
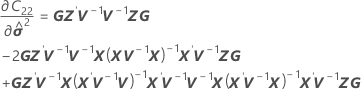
Notation
| Term | Description |
|---|---|
| W | the asymptotic variance-covariance matrix of 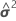 |
For further details on the notation, go to Conditional fits and residuals in Fit Mixed Effects Model.
Conditional prediction interval
The conditional prediction interval is:

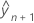 is the conditional fit at the new variable setting.
is the conditional fit at the new variable setting.
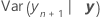 =
= 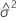
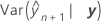 =
= 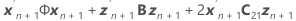
The degrees of freedom use this formula for the conditional case:
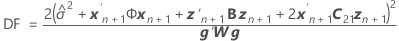
where
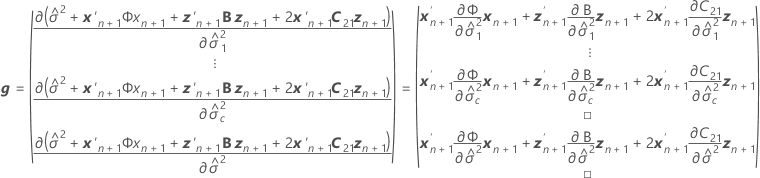
Notation
| Term | Description |
|---|---|
| W | the asymptotic variance-covariance matrix of the variance component estimates |
| I | the identity matrix |
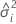 | the variance component for the ith random effect term |
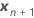 | the vector of the new settings for the fixed effect terms |
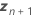 | the vector of the new settings for the random terms |
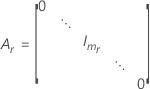
| c | the number of random terms in the model |
| B |
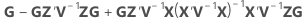 |
 |
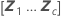 |
| C21 |
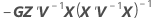 |
| G |
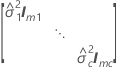 |
| mi | the number of levels for the 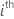 random effect random effect |
| X | the n x p design matrix for the fixed effects terms,  |
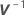 | the inverse of the variance-covariance matrix |
 | the n x mi design matrix for the 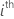 random term in the model random term in the model |
