In This Topic
Conditional fits
The conditional fits are the estimates for the mean response values at both the fixed and the random factor settings given in the data set. The conditional fits are calculated from the conditional fitted equations.
SE Fit
The standard error of the fit (SE fit) estimates the variation in the estimated mean response for the specified variable settings. The calculation of the confidence interval for the mean response uses the standard error of the fit. Standard errors are always non-negative.
DF for conditional mean
The degrees of freedom (DF) represent the amount of information in the data to estimate the confidence interval for the mean response.
Interpretation
Use the DF to compare how much information is available about different conditional means. Generally, more degrees of freedom make the confidence interval for the mean narrower than an interval with less degrees of freedom. Because the standard errors for the means for different observations are different, the confidence interval for a mean with more degrees of freedom does not have to be narrower than a confidence interval for a mean with fewer degrees of freedom.
Confidence interval for conditional mean (95% CI)
These confidence intervals (CI) are ranges of values that are likely to contain the corresponding conditional mean responses.
Because samples are random, two samples from a population are unlikely to yield identical confidence intervals. But, if you sample many times, a certain percentage of the resulting confidence intervals contain the unknown population parameter. The percentage of these confidence intervals that contain the parameter is the confidence level of the interval.
- Point estimate
- The point estimate is the estimate of the parameter that is calculated from the sample data. The confidence interval is centered around this value.
- Margin of error
- The margin of error defines the width of the confidence interval and is determined by the observed variability in the sample, the sample size, and the confidence level. To calculate the upper limit of the confidence interval, the error margin is added to the point estimate. To calculate the lower limit of the confidence interval, the error margin is subtracted from the point estimate.
Interpretation
Use the confidence intervals to evaluate whether the conditional mean responses are statistically larger than, equal to, or less than a specific value. You can also use the confidence intervals to determine a range of values for the corresponding unknown conditional mean responses.
Conditional resid
A residual (ei) is the difference between an observed value (y) and the corresponding conditional fitted value, (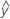 ).
).
Interpretation
Plot the residuals to determine whether your model is adequate and meets the assumptions of mixed effects model. Examining the residuals can provide useful information about how well the model fits the data. In general, the residuals should be randomly distributed with no obvious patterns and no unusual values. If Minitab determines that your data include unusual observations, it identifies those observations in the Conditional Fits and Diagnostics for Unusual Observations table in the output. The observations that Minitab labels as unusual do not follow the proposed conditional equation well. However, it is expected that you will have some unusual observations. For example, based on the criteria for large residuals, you would expect roughly 5% of your observations to be flagged as having a large residual.
Std Resid
The standardized conditional residual equals the value of a residual (ei) divided by an estimate of its standard deviation.
Interpretation
Use the standardized conditional residuals to help you detect outliers. Standardized conditional residuals greater than 2 and less than −2 are usually considered large. The Conditional Fits and Diagnostics for Unusual Observations table identifies these observations with an 'R'. The observations that Minitab labels do not follow the proposed conditional fitted equation well. However, it is expected that you will have some unusual observations. For example, based on the criteria for large standardized conditional residuals, you would expect roughly 5% of your observations to be flagged as having a large standardized residual.
Standardized conditional residuals are useful because raw conditional residuals might not be good indicators of outliers. The variance of each raw conditional residual can differ by the x-values associated with it. This unequal variation causes it to be difficult to assess the magnitudes of the raw conditional residuals. Standardizing the conditional residuals solves this problem by converting the different variances to a common scale.
