Box-Cox transformation (λ)
If you include the Box-Cox transformation when you perform individual distribution identification, Minitab reports the value of lambda (λ) used in the transformation.
The Box-Cox transformation estimates a lambda value, as shown below, which minimizes the standard deviation of a standardized transformed variable. The resulting transformation is Yλ when λ ҂ 0 and ln Y when λ = 0.
This method searches through many types of transformations. The following table shows some common transformations, where Y' is the transform of the data Y:
| Lambda (λ) value | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
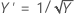 |
 |
 |
Johnson transformation function
If you include the Johnson transformation when you perform individual distribution identification, Minitab reports the function used to transform the data. For example, suppose the Johnson transformation function is 0.762475 + 0.870902 × Ln(( X – 46.3174)/(59.6770 – X)). If the original data value for X is 50, then the transformed value of 50 is calculated as 0.762475 + 0.870902 × Ln((50 – 46.3174)/(59.6770 – 50)), which equals –0.07893.
For more information on the algorithm that Minitab uses to define the Johnson transformation function, go to Methods and formulas for transformations in Individual Distribution Identification.
