Capability indices for Johnson transformed data
The Johnson transformation optimally selects a function from three families of distributions of a variable, which are easily transformed into a standard normal distribution. These distributions are labeled SB, SL, and SU, where B, L, and U refer to the variable being bounded, lognormal, and unbounded. Minitab identifies the parameters for the distributions as first shape, second shape, location, and scale. For more information, go to Methods and formulas for transformations in Individual Distribution Identification and click "Methods and formulas for the Johnson transformation".
When both specification limits are in the range of the transformation function, Minitab calculates the overall capability indices based on normal distribution for the transformed data. For more information, go to Methods and formulas for overall capability measures in Normal Capability Analysis.
When the selected family is the SB or SL type and the lower and/or the upper specification limit is outside the distribution range, Minitab performs additional calculations to generate the overall capability indices.
SB Distribution
If at least one of the specification limits (X) is outside the distribution range (not ε < X < ε + λ) before the transformation, Pp, Ppk, PPL, PPU, Z.LSL, and Z.USL are calculated as follows.
First, Minitab calculates the percentiles in the transformed space.
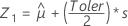
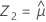
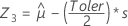
Using the three Z values, Minitab calculates the corresponding X1, X2, and X3 values in the original space:
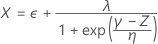
The overall capability indices are then calculated from the X values and the values of the specification limits.

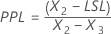

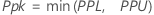


Notation
| Term | Description |
|---|---|
| LSL | Lower specification limit |
| USL | Upper specification limit |
 | Sample mean (X̅) of the transformed data |
| Toler | Tolerance in standard deviations |
| s | Sample standard deviation of the transformed data |
| ε, | Location parameter of the Johnson transformation |
| γ | Shape parameter of the Johnson transformation |
| η | Shape parameter of the Johnson transformation (η >0) |
| λ | Scale parameter of the Johnson transformation (λ > 0) |
The calculations for Z.Bench and the expected performance values for an SB distribution depend on the locations of LSL and USL relative to X2 and the distribution limits.
- LSL and USL are on opposite sides of X2
-
- When both LSL and USL are outside the distribution range, Minitab displays the following:
Z.Bench is missing
PPM < LSL = 0
PPM > USL = 0
PPM Total = 0
- When one specification limit is outside the distribution range and the other specification limit is inside the distribution range, Minitab calculates the following values:

PPM for specification limit outside the range = 0
PPM for specification limit inside the range = p*1000000
PPM Total = p*1000000
Note
Minitab uses the transformed data and the transformed specification limits to calculate PPM.
- When both LSL and USL are outside the distribution range, Minitab displays the following:
- LSL and USL are on the left of X2
-
- When both LSL and USL are outside the distribution range, Minitab displays the following:
Z.Bench is missing
PPM < LSL = 0
PPM > USL = 1
PPM Total = 1
- When LSL is outside the distribution range and USL is inside the distribution range, Minitab calculates the following values:

PPM < LSL = 0
PPM > USL = p*1000000
PPM Total = PPM > USL
Note
Minitab uses the transformed data and transformed specification limits to calculate PPM.
- When both LSL and USL are outside the distribution range, Minitab displays the following:
- LSL and USL are on the right of X2
-
- When both LSL and USL are outside the distribution range, Minitab displays the following:
Z.Bench is missing
PPM < LSL = 1
PPM > USL = 0
PPM Total = 1
- When LSL is inside the distribution range and USL is outside the distribution range, Minitab calculates the following values.

PPM < LSL = p*1000000
PPM > USL = 0
PPM Total = PPM < LSL
Note
Minitab uses the transformed data and the transformed specification limits to calculate PPM.
- When both LSL and USL are outside the distribution range, Minitab displays the following:
SL Distribution
If at least one of the specification limits is outside the distribution range before the transformation, Minitab uses the same method as shown above for the SB Distribution to calculate Pp, Ppk, PPL, PPU, Z.LSL, and Z.USL. The only change is the formula for finding the original value X from the transformed value Z.

- LSL and USL are less than or equal to ε (both are outside the distribution range)
-
Z.Bench is missing
PPM < LSL = 0
PPM > USL = 1
PPM Total = 1
- LSL is less than or equal to ε
-

PPM < LSL = 0
PPM > USL = p*1000000
PPM Total = PPM > USL
Notation
| Term | Description |
|---|---|
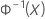 | Inverse cumulative distribution function (cdf) of a standard normal distribution |
| p | Probability of the transformed data being outside the transformed specification limit |
