Use the beta distribution for random variables between 0 and 1. The beta distribution is frequently used to model the distribution of order statistics—for example, the kth order statistic from a sample of n uniform (0, 1) variables has a beta (k, n + 1 – k) distribution—and to model events that are defined by minimum and maximum values. The beta distribution is often rescaled to model the time to completion of a task. The beta distribution is also used in Bayesian statistics, for example, as the prior distribution of a binomial probability.
The beta distribution is a continuous distribution defined by two shape parameters. The distribution can take on different shapes depending on the values of the two parameters.
- Both shapes equal 1
-
When both shapes equal 1, the beta distribution is the uniform distribution.

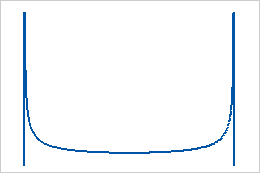
- Both shapes are less than 1
-
When both shapes are less than 1, the distribution is U-shaped.
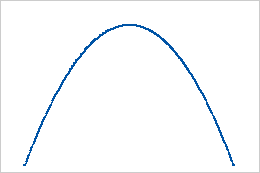
- Both shapes are the same and are greater than 1
-
When both shapes are equal and greater than 1, the distribution is symmetric.
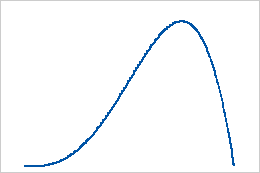
- First shape is greater than second shape
-
When the first shape is greater than the second shape, the distribution is skewed to the left.
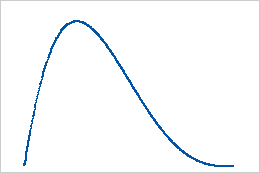
- First shape is less than second shape
-
When the first shape is less than second shape, the distribution is skewed to the right.