In This Topic
Number of concordant and discordant pairs
A pair is concordant if the observation ranking higher on variable X also ranks higher on variable Y. The pair is discordant if the observation ranking higher on X ranks lower on Y. The pair is tied if the subjects have the same classification on X and/or Y.
Formula


Notation
| Term | Description |
|---|---|
| nij | observations in the cell corresponding to the ith row and jth column |
Gamma
Goodman and Kruskal's gamma is a measure of association between the ordinal variables. Perfect association exists when |γ| = 1. If X and Y are independent, γ = 0.
Formula

Notation
| Term | Description |
|---|---|
| C | number of concordant pairs = Σi<kΣj<l nij nkl |
| D | number of discordant pairs = Σi<kΣj>l nij nkl |
| nij | observations in the cell corresponding to ith row and jth column |
Somers' D
Somers' D measures the strength and direction of the relationship between two ordinal variables.
Formula
With Y as the response variable:

With X as the response variable:

Notation
| Term | Description |
|---|---|
| TX | number of pairs tied on X = 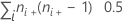 |
| TY | number of pairs tied on Y = 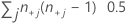 |
| C | number of concordant pairs |
| D | number of discordant pairs |
| ni+ | number of observations in the ith row |
| n+j | number of observations in the jth column |
| nij | observations in the cell corresponding to the ith row and jth column |
| n++ | total number of observations |
Kendall's Tau-b
Kendall's tau-b, like gamma, measures the association between ordinal variables. One strength of Kendall's tau-b as a measure of association is that it accounts for tied pairs in its calculation. Gamma has a problem with tied pairs, so gamma almost always shows a higher association than tau-b. The tau-b values range from -1.0 to 1.0.
Formula

Notation
| Term | Description |
|---|---|
| TX | number of pairs tied on X = Σi ni+ (ni+- 1) 0.5 |
| TY | number of pairs tied on Y = Σj n+j (n+j- 1) 0.5 |
| C | number of concordant pairs = Σi<kΣj<l nij nkl |
| D | number of discordant pairs = Σi<kΣj>l nij nkl |
| ni+ | number of observations in the ith row |
| n+j | number of observations in the jth column |
| nij | observations in the cell corresponding to ith row and jth column |
| n++ | total number of observations |
Test of concordance
The test of concordance is a test of independence. The p-value is a probability that measures the evidence against the null hypothesis. Lower probabilities provide stronger evidence against the null hypothesis.
Formula
The test of concordance uses a standard normal test statistic:

The p-value equals the probability that Z is greater than Z*.
Notation
| Term | Description |
|---|---|
| C | number of concordant pairs = Σi<kΣj<l nij nkl |
| D | number of discordant pairs = Σi<kΣj>l nij nkl |
| SE(C-D) | Standard error or C-D, which approximately equals 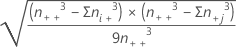 |
| n++ | the total number of observations |
| ni+ | the number of observations in the ith row. |
| n+j | the number of observations in the jth column. |
