The manager of a lumber yard wants to assess the performance of a saw mill that cuts beams that are supposed to be 100 cm long. The manager plans to perform a 1 variance test to determine the variability of the mill.
Before collecting the data for a 1 variance test, the manager uses a power and sample size calculation to determine what the power of the test will be when the sample sizes are 50 and 100 and the test detects a 0.8 ratio between the comparison and hypothesized standard deviations.
- Choose .
- In Sample sizes, enter 50 100.
- In Ratios, enter 0.8.
- Click OK.
Interpret the results
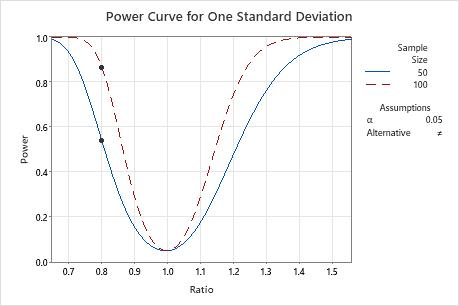
To detect a ratio of 0.8, the analyst can obtain a power of 0.539 with a sample size of 50 and a power of 0.865 with a sample size of 100. To have enough power to detect a ratio of 0.8, the analyst decides to collect 100 samples.
Results
| Ratio | Sample Size | Power |
|---|---|---|
| 0.8 | 50 | 0.539065 |
| 0.8 | 100 | 0.865153 |