A healthcare consultant wants to compare the patient satisfaction ratings of two hospitals. The consultant collects ratings from 20 patients for each of the hospitals.
The consultant performs a 2 variances test to determine whether the standard deviations in the patient ratings from the two hospitals differ.
- Open the sample data, HospitalComparison.MTW.
- Choose .
- From the drop-down list, select Both samples are in one column.
- In Samples, enter Rating.
- In Sample IDs, enter Hospital.
- Click OK.
Interpret the results
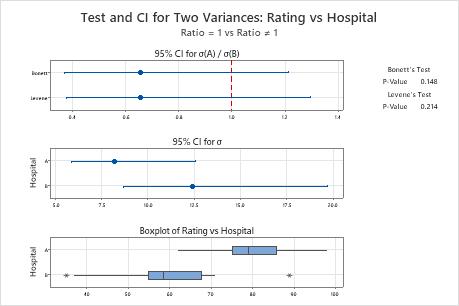
The null hypothesis states that the ratio between the standard deviations is 1. Because the p-values are both greater than the significance level (denoted as α or alpha) of 0.05, the consultant fails to reject the null hypothesis. The consultant does not have enough evidence to conclude that the standard deviations between the hospitals are different.
Test and CI for Two Variances: Rating vs Hospital
Method
σ₁: standard deviation of Rating when Hospital = A
σ₂: standard deviation of Rating when Hospital = B
Ratio: σ₁/σ₂
The Bonett and Levene's methods are valid for any continuous distribution.
Descriptive Statistics
Hospital N StDev Variance 95% CI for σ
A 20 8.183 66.958 (5.893, 12.597)
B 20 12.431 154.537 (8.693, 19.709)
Ratio of Standard Deviations
95% CI for 95% CI for
Estimated Ratio using Ratio using
Ratio Bonett Levene
0.658241 (0.372, 1.215) (0.378, 1.296)
Test
Null hypothesis H₀: σ₁ / σ₂ = 1
Alternative hypothesis H₁: σ₁ / σ₂ ≠ 1
Significance level α = 0.05
Test
Method Statistic DF1 DF2 P-Value
Bonett 2.09 1 0.148
Levene 1.60 1 38 0.214
