In This Topic
Null hypothesis and alternative hypothesis
- Null hypothesis
- The null hypothesis states that a population parameter (such as the mean, the standard deviation, and so on) is equal to a hypothesized value. The null hypothesis is often an initial claim that is based on previous analyses or specialized knowledge.
- Alternative hypothesis
- The alternative hypothesis states that a population parameter is smaller, larger, or different from the hypothesized value in the null hypothesis. The alternative hypothesis is what you might believe to be true or hope to prove true.
Interpretation
In the output, the null and alternative hypotheses help you to verify that you entered the correct value for the hypothesized standard deviation or hypothesized variance.
N
The sample size (N) is the total number of observations in the sample.
Interpretation
The sample size affects the confidence interval and the power of the test.
Usually, a larger sample size results in a narrower confidence interval. A larger sample size also gives the test more power to detect a difference. For more information, go to What is power?.
StDev
The standard deviation is the most common measure of dispersion, or how spread out the data are about the mean. The symbol σ (sigma) is often used to represent the standard deviation of a population, while s is used to represent the standard deviation of a sample. Variation that is random or natural to a process is often referred to as noise.
The standard deviation uses the same units as the data.
Interpretation
The standard deviation of the sample data is an estimate of the population standard deviation.
Because the standard deviation is based on sample data and not on the entire population, it is unlikely that the sample standard deviation equals the population standard deviation. To better estimate the population standard deviation, use the confidence interval.
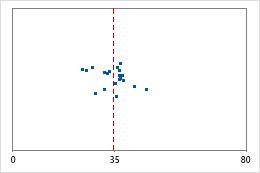
Hospital 1
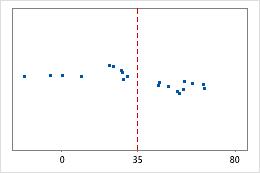
Hospital 2
Hospital discharge times
Administrators track the discharge time for patients who are treated in the emergency departments of two hospitals. Although the average discharge times are about the same (35 minutes), the standard deviations are significantly different. The standard deviation for hospital 1 is about 6. On average, a patient's discharge time deviates from the mean (dashed line) by about 6 minutes. The standard deviation for hospital 2 is about 20. On average, a patient's discharge time deviates from the mean (dashed line) by about 20 minutes.
Variance
The variance measures how spread out the data are about their mean. The variance is equal to the standard deviation squared.
Interpretation
The variance of the sample data is an estimate of the population variance.
Because the variance is based on sample data and not on the entire population, it is unlikely that the sample variance equals the population variance. To better estimate the population variance, use the confidence interval.
Confidence interval (CI) and bounds
The confidence interval provides a range of likely values for the population standard deviation or the population variance. Because samples are random, two samples from a population are unlikely to yield identical confidence intervals. But, if you repeated your sample many times, a certain percentage of the resulting confidence intervals or bounds would contain the unknown population standard deviation or population variance. The percentage of these confidence intervals or bounds that contain the standard deviation or the variance is the confidence level of the interval. For example, a 95% confidence level indicates that if you take 100 random samples from the population, you could expect approximately 95 of the samples to produce intervals that contain the population standard deviation or the population variance.
An upper bound defines a value that the population standard deviation or population variance is likely to be less than. A lower bound defines a value that the population standard deviation or population variance is likely to be greater than.
The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. If the interval is too wide to be useful, consider increasing your sample size. For more information, go to Ways to get a more precise confidence interval.
Note
When you enter a column of data, Minitab only calculates a confidence interval for the standard deviation.
Note
Minitab cannot calculate the Bonett method with summarized data.
Descriptive Statistics
| N | StDev | Variance | 95% CI for σ using Bonett | 95% CI for σ using Chi-Square |
|---|---|---|---|---|
| 50 | 0.871 | 0.759 | (0.704, 1.121) | (0.728, 1.085) |
In these results, the estimate of the population standard deviation for the length of beams is 0.871, and the estimate of the population variance is 0.759. Because the data did not pass a normality test, use the Bonett method. You can be 95% confident that the population standard deviation is between 0.704 and 1.121.
Test statistic
The test statistic is a statistic for chi-square tests that measures the ratio between an observed variance and its hypothesized variance.
Interpretation
You can compare the test statistic to critical values of the chi-square distribution to determine whether to reject the null hypothesis. However, using the p-value of the test to make the same determination is usually more practical and convenient. The p-value has the same meaning for any size test, but the same chi-square statistic can indicate opposite conclusions depending on the sample size.
- For a two sided test, the critical values are
 and
and 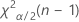 . If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If it is in between, you fail to reject the null hypothesis.
. If the test statistic is less than the first value or greater than the second value, you reject the null hypothesis. If it is in between, you fail to reject the null hypothesis. - For a one sided test with an alternative hypothesis of less than, the critical value is
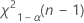 . If the test statistic is less than the value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is less than the value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis. - For a one sided test of greater than, the critical value is
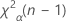 . If the test statistic is greater than the value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
. If the test statistic is greater than the value, you reject the null hypothesis. If it is not, you fail to reject the null hypothesis.
The test statistic is used to calculate the p-value. Because there is no test statistic for the Bonnet method, Minitab uses the rejection regions that are defined by the confidence limits to calculate a p-value.
DF
The degrees of freedom (DF) indicate the amount of information that is available in your data to estimate the values of the unknown parameters, and to calculate the variability of these estimates. For a 1 variance test, the degrees of freedom are determined by the number of observations in your sample.
Interpretation
Minitab uses the degrees of freedom to determine the test statistic. The degrees of freedom are determined by the sample size. Increasing your sample size provides more information about the population, which increases the degrees of freedom.
P-Value
The p-value is a probability that measures the evidence against the null hypothesis. A smaller p-value provides stronger evidence against the null hypothesis.
Interpretation
Use the p-value to determine whether the population variance or standard deviation is statistically different from the hypothesized variance or standard deviation.
- P-value ≤ α: The difference between the variances or standard deviations is statistically significant (Reject H0)
- If the p-value is less than or equal to the significance level, the decision is to reject the null hypothesis. You can conclude that the difference between the population variance or standard deviation the hypothesized variance or standard deviation is statistically significant. Use your specialized knowledge to determine whether the difference is practically significant. For more information, go to Statistical and practical significance.
- P-value > α: The difference between the variances or standard deviations is not statistically significant (Fail to reject H0)
- If the p-value is greater than the significance level, the decision is to fail to reject the null hypothesis. You do not have enough evidence to conclude that the difference between the population variance or standard deviation and the hypothesized variance or standard deviation is statistically significant. You should make sure that your test has enough power to detect a difference that is practically significant. For more information, go to Power and Sample Size for 1 Variance.
Note
When you have summarized data, Minitab cannot calculate a p-value for the Bonett method.
