Model order is the type of model used to show a trend in the data. The model order is an important factor in how accurately the model describes the data and predicts a response.
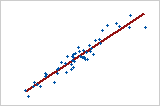
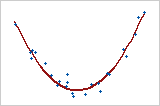
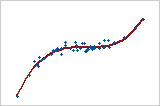
For example, a linear model can show a steady rate of increase or decrease in the data. A quadratic model (often approximately in the shape of a U or an inverted U) can explain curvature in the data. A cubic model can describe a "peak-and-valley" pattern in the data.
| Model order | Example |
|---|---|
|
Linear Y = bo + b1X (first order) |
|
|
Quadratic Y = bo + b1X + b11X2 (second order) |
|
|
Cubic Y = bo + b1X + b11X2 + b111 X3 (third order) |
|
Each model order corresponds with the degree of the equation (the highest power of the X variable) used to generate the model, where Y is the response, X is the predictor, bo is the intercept, and b1, b11, and b111 are the coefficients.