In This Topic
Shelf life for a model with a random batch factor and only a lower specification limit
To simplify the calculation of the shelf life, consider whether the model includes the time*batch interaction or not.
The model with time, batch, and the time*batch interaction
When the batch effect and the batch*time interaction are in the model, the fit for the ith batch at time xij uses this model:
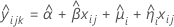
| Term | Description |
|---|---|
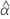 | the estimated fixed mean intercept for all batches |
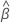 | the estimated mean slope for all batches |
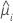 | the estimated random intercept for the ith batch |
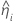 | the estimated slope for the ith batch |
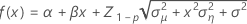
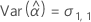

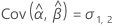


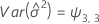
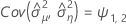
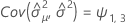
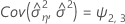
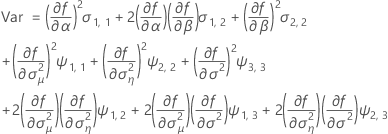
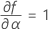
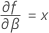

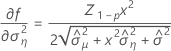

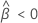
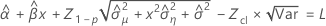
Minitab uses an iterative algorithm to find a solution between 0 and 10 times the largest value in the time variable.
The model with time and batch
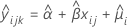
| Term | Description |
|---|---|
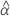 | the estimated fixed mean intercept for all batches |
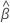 | the estimated mean slope for all batches |
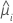 | the estimated random intercept for the ith batch |
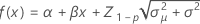
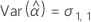

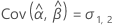

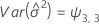
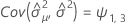
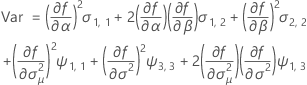
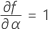
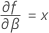
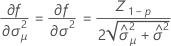
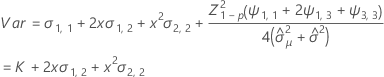
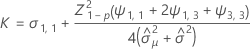

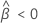
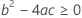

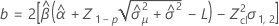



Notation
| Term | Description |
|---|---|
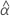 | the estimated fixed mean intercept for all batches |
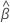 | the estimated mean slope for all batches |
| Z | the value of the inverse cumulative distribution function |
| L | the lower specification limit |
| x | the shelf life |
| p | the proportion of the product above the lower specification limit |
| X | the design matrix |
Shelf life for a model with a random batch factor and only an upper specification limit
To simplify the calculation of the shelf life, consider whether the model includes the time*batch interaction or not.
The model with time, batch, and the time*batch interaction
When the batch effect and the batch*time interaction are in the model, the fit for the ith batch at time xij uses this model:
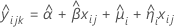
| Term | Description |
|---|---|
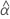 | the estimated fixed mean intercept for all batches |
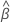 | the estimated mean slope for all batches |
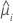 | the estimated random intercept for the ith batch |
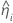 | the estimated slope for the ith batch |

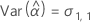

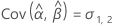


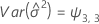
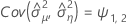
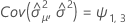
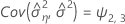
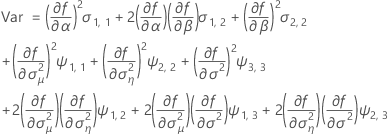
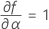
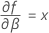

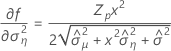

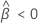
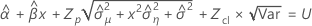
Minitab uses an iterative algorithm to find a solution between 0 and 10 times the largest value in the time variable.
The model with time and batch
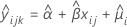
| Term | Description |
|---|---|
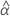 | the estimated fixed mean intercept for all batches |
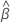 | the estimated mean slope for all batches |
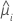 | the estimated random intercept for the ith batch |
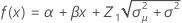
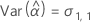

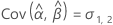

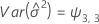
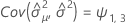
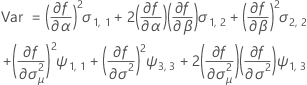
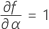
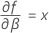
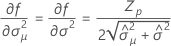
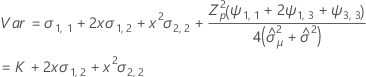
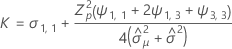

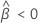
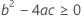



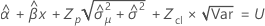

Notation
| Term | Description |
|---|---|
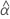 | the estimated fixed mean intercept for all batches |
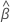 | the estimated mean slope for all batches |
| Z | the value of the inverse cumulative distribution function |
| L | the lower specification limit |
| x | the shelf life |
| p | the proportion of the product above the lower specification limit |
| X | the design matrix |
Both limits
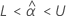
If a meaningful estimate exists, then Minitab determines whether to estimate the shelf life relative to the upper specification limit or the lower specification limit.
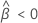

For details on the calculation of the shelf life for each case, go to the section that describes the calculation when there is only one specification limit. To calculate the shelf life when the calculations have two limits that are both relevant to the shelf life, change Zcl and Z0.95 to Z0.5+cl/2.
Notation
| Term | Description |
|---|---|
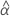 | the estimated fixed mean intercept for all batches |
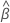 | the estimated mean slope for all batches |
| cl | the confidence level |
