In This Topic
Polynomial regression models
Formula
You can fit the following linear, quadratic, or cubic regression models:
| Model type | Order | Statistical model |
|---|---|---|
| linear | first | Y = β0+ β1x + e |
| quadratic | second | Y = β0+ β1x + β2x2+ e |
| cubic | third | Y = β0+ β1x + β2x2+ β3x3+ e |
Another way of modeling curvature is to generate additional models by using the log10 of x and/or y for linear, quadratic, and cubic models. In addition, taking the log10 of Y may be used to reduce right-skewness or nonconstant variance of residuals.
When Minitab fits the quadratic or cubic models, Minitab standardizes the predictors before it estimates the coefficients. The standardization reduces the multicollinearity among the predictors. The reduction ensures that the multicollinearity is so low that Minitab is unlikely to exclude any predictors from the model. The output shows the unstandardized coefficients in the original units of the predictors."
Coefficient (Coef)
The formula for the coefficient or slope in simple linear regression is:
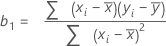
The formula for the intercept (b0) is:

In matrix terms, the formula that calculates the vector of coefficients in multiple regression is:
b = (X'X)-1X'y
Notation
| Term | Description |
|---|---|
| yi | ith observed response value |
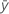 | mean response |
| xi | ith predictor value |
 | mean predictor |
| X | design matrix |
| y | response matrix |
S

Notation
| Term | Description |
|---|---|
| MSE | mean square error |
R-sq


R2 can also be calculated as the squared correlation of y and 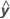 .
.
Notation
| Term | Description |
|---|---|
| SS | Sum of Squares |
| y | response variable |
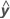 | fitted response variable |
R-sq (adj)

Notation
| Term | Description |
|---|---|
| MS | Mean Square |
| SS | Sum of Squares |
| DF | Degrees of Freedom |
Degrees of freedom (DF)
The degrees of freedom for each component of the model are:
| Sources of variation | DF |
|---|---|
| Regression | p |
| Error | n – p – 1 |
| Total | n – 1 |
- The data contain multiple observations with the same predictor values.
- The data contain the correct points to estimate additional terms that are not in the model.
Notation
| Term | Description |
|---|---|
| n | number of observations |
| p | number of coefficients in the model, not counting the constant |
Adj SS
The sum of the squared distances. SS Regression is the portion of the variation explained by the model. SS Error is the portion not explained by the model and is attributed to error. SS Total is the total variation in the data.
Formula

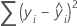
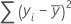
Notation
| Term | Description |
|---|---|
| yi | i th observed response value |
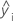 | i th fitted response |
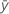 | mean response |
Adj MS – Error
The Mean Square of the error (also abbreviated as MS Error or MSE, and denoted as s2) is the variance around the fitted regression line. The formula is:

Notation
| Term | Description |
|---|---|
| yi | ith observed response value |
 | ith fitted response |
| n | number of observations |
| p | number of coefficients in the model, not counting the constant |
Adj MS – Regression
The formula for the Mean Square (MS) of the regression is:
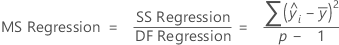
Notation
| Term | Description |
|---|---|
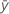 | mean response |
 | ith fitted response |
| p | number of terms in the model |
Adj MS – Total
The formula for the total Mean Square (MS) is:
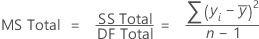
Notation
| Term | Description |
|---|---|
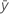 | mean response |
| yi | ith observed response value |
| n | number of observations |
F-value
The formulas for the F-statistics are as follows:
- F(Regression)
-

- F(Term)
-

- F(Lack-of-fit)
-

Notation
| Term | Description |
|---|---|
| MS Regression | A measure of the variation in the response that the current model explains. |
| MS Error | A measure of the variation that the model does not explain. |
| MS Term | A measure of the amount of variation that a term explains after accounting for the other terms in the model. |
| MS Lack-of-fit | A measure of variation in the response that could be modeled by adding more terms to the model. |
| MS Pure error | A measure of the variation in replicated response data. |
P-value – Analysis of variance table
The p-value is a probability that is calculated from an F-distribution with the degrees of freedom (DF) as follows:
- Numerator DF
- sum of the degrees of freedom for the term or the terms in the test
- Denominator DF
- degrees of freedom for error
Formula
1 − P(F ≤ fj)
Notation
| Term | Description |
|---|---|
| P(F ≤ f) | cumulative distribution function for the F-distribution |
| f | f-statistic for the test |
Residual (Resid)
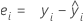
Notation
| Term | Description |
|---|---|
| ei | i th residual |
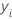 | i th observed response value |
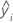 | i th fitted response |
