Note
This command is available with the Predictive Analytics Module. Click here for more information about how to activate the module.
TreeNet® models are an approach to solving classification and regression problems that are both more accurate and resistant to overfitting than a single classification or regression tree. A broad, general description of the process is that we begin with a small regression tree as an initial model. From that tree come residuals for every row in the data which become the response variable for the next regression tree. We build another small regression tree to predict the residuals from the first tree and compute the resulting residuals again. We repeat this sequence until an optimal number of trees with minimum prediction error is identified using a validation method. The resulting sequence of trees makes the TreeNet® Regression Model.
For the regression case, we can add a general description of the analysis, but some details depend on which of the following is the loss function:
| Statistic | Value |
|---|---|
Initial fit, 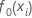
|
mean of the response variable |
Generalized residual,
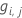 as response value for row
i
as response value for row
i
|

|
Within node updates,

|
mean of 
|
| Statistic | Value |
|---|---|
Initial fit, 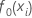
|
median of the response variable |
Generalized residual,
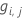 as response value for row
i
as response value for row
i
|

|
Within node updates,

|
median of 
|
Huber loss function
For the Huber loss function, the statistics are as follows:
The initial fit, 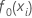 ,
equals the median of all response values.
,
equals the median of all response values.
For growing the jth tree, 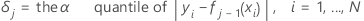
Then, the generalized residual for the ith row is as follows:
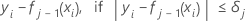

The generalized residuals are used as the response values to grow the jth tree.
The updated value for rows in the mth terminal node of the jth tree is as follows:
 to be the regular residual for the
ith row after
j-1 trees are grown. Let
to be the regular residual for the
ith row after
j-1 trees are grown. Let 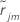 be the median of the
be the median of the 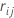 values for rows inside terminal node
m of the
jth tree. Then, the updated value for every row inside the
mth terminal node of the
jth tree is:
values for rows inside terminal node
m of the
jth tree. Then, the updated value for every row inside the
mth terminal node of the
jth tree is: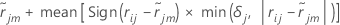
The mean in the previous expression is calculated across all the rows inside the terminal node m of the jth tree.
Notation for loss functions
In the preceding details, 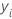 is the value of the response variable for row
i,
is the value of the response variable for row
i,  is the fitted value from the previous
j – 1 trees, and
is the fitted value from the previous
j – 1 trees, and 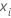 is a vector that represents the
ith row of the predictor values in the training data.
is a vector that represents the
ith row of the predictor values in the training data.
Input parameters
| Input | Symbol |
|---|---|
| learn rate |  |
| sampling rate | 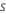 |
| maximum number of terminal nodes per tree | 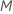 |
| number of trees | 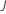 |
| switching value |  |
General process
- Draw a random sample of size s * N from the training data, where N is the number of rows in the training data.
- Calculate the generalized
residuals,
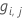 ,
for
,
for  .
.
- Fit a regression tree with at most M terminal nodes to the generalized residuals. The tree partitions the observations into at most M mutually exclusive groups.
- For the
mth terminal node in the regression tree, calculate the
within-node updates to the tree that depend on the loss function,
 .
.
- Shrink the within-node
updates by the learning rate and apply the values to get the updated fitted
values,
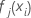 :
:
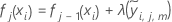
- Repeat steps 1-5 for each of the J trees in the analysis.
