Note
This command is available with the Predictive Analytics Module. Click here for more information about how to activate the module.
 and
and 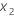 are two predictor variables. Minitab provides two measures of the strengths of
interactions. The measures come from the training data. The first measure
describes the strength of the interaction as a percentage of the total response
squared deviation:
are two predictor variables. Minitab provides two measures of the strengths of
interactions. The measures come from the training data. The first measure
describes the strength of the interaction as a percentage of the total response
squared deviation: 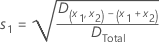
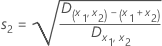
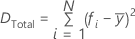
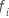 is the fitted value from the TreeNet model and
is the fitted value from the TreeNet model and
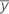 has the following definition:
has the following definition: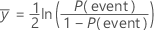

where  is the number of events in the training data.
is the number of events in the training data.
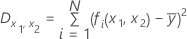
where 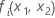 is the fitted value from a bivariate partial dependence surface. For the
calculation of this fitted value, go to
Methods and formulas for partial dependence plots in Fit Model and Discover Key Predictors with TreeNet® Classification.
is the fitted value from a bivariate partial dependence surface. For the
calculation of this fitted value, go to
Methods and formulas for partial dependence plots in Fit Model and Discover Key Predictors with TreeNet® Classification.
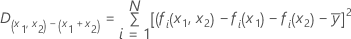
where 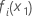 and
and 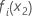 are fitted values from univariate partial dependence surfaces for
are fitted values from univariate partial dependence surfaces for
 and
and 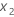 .
For the calculation of these fitted values, go to
Methods and formulas for partial dependence plots in Fit Model and Discover Key Predictors with TreeNet® Classification.
.
For the calculation of these fitted values, go to
Methods and formulas for partial dependence plots in Fit Model and Discover Key Predictors with TreeNet® Classification.
