In This Topic
Pearson residuals
Elements of the Pearson chi-square that can be used to detect ill-fitted factor/covariate patterns. Minitab stores the Pearson residual for the ith factor/covariate pattern. The formula is:
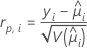
Notation
| Term | Description |
|---|---|
| yi | the response value for the ith factor/covariate pattern |
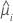 | the fitted value for the ith factor/covariate pattern |
| V | the variance function for the model at 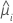 |
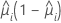
Standardized and deleted Pearson residuals
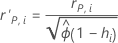
Notation
| Term | Description |
|---|---|
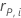 | the Pearson residual for the ith factor/covariate pattern |
 | 1, for binomial models |
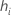 | the leverage for the ith factor/covariate pattern |
Deviance residuals
Deviance residuals are based on the model deviance and are useful in identifying ill-fitted factor/covariate patterns. The model deviance is a goodness-of-fit statistic based on the log-likelihood function. The deviance residual defined for the ith factor/covariate pattern is:

Notation
| Term | Description |
|---|---|
| yi | the response value for the ith factor/covariate pattern |
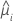 | the fitted value for the ith factor/covariate pattern |
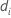 | the deviance for the ith factor/covariate pattern |
Standardized deviance residual

Notation
| Term | Description |
|---|---|
| rD,i | The deviance residual for the ith factor/covariate pattern |
| hi | The leverage for the ith factor/covariate pattern |
Deleted deviance residual

Notation
| Term | Description |
|---|---|
| yi | the response value at the ith factor/covariate pattern |
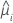 | the fitted value for the ith factor covariate pattern |
| hi | the leverage for the ith factor/covariate pattern |
| r'D,i | the standardized deviance residual for the ith factor/covariate pattern |
| r'P,i | the standardized Pearson residual for the ith factor/covariate pattern |
1. Pregibon, D. (1981). "Logistic Regression Diagnostics." The Annals of Statistics, Vol. 9, No. 4 pp. 705–724.
Delta chi-square
Minitab calculates the change in the Pearson chi-square due to deleting all the observations with the jth factor/covariate pattern. Minitab stores one delta chi-square value for each distinct factor/covariate pattern in the data. You can use delta chi-square to detect ill-fitted factor/covariate patterns. The formula for the delta chi-square is:
Formula
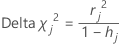
Notation
| Term | Description |
|---|---|
| hj | leverage |
| rj | Pearson residuals |
Delta deviance
Minitab calculates the change in the deviance statistic by deleting all the observations with the jth factor/covariate pattern. Minitab stores one value for each distinct factor/covariate pattern in the data. You can use delta deviance to detect ill-fitted factor/covariate patterns. The change in the deviance statistic is:
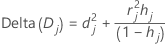
Notation
| Term | Description |
|---|---|
| hj | leverage |
| rj | Pearson residuals |
| dj | deviance residuals |
Delta beta (standardized)
Minitab calculates the change by deleting all observations with the jth factor/covariate pattern. One value is stored for each distinct factor/covariate pattern in the data. You can use standardized delta β to detect factor/covariate patterns that have a strong influence on the estimates of the coefficients. This value is based on the standardized Pearson residual.
Formula
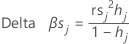
Notation
| Term | Description |
|---|---|
| hj | leverage |
| rs j | standardized Pearson residuals |
Delta beta
Minitab calculates the change by deleting all observations with the jth factor/covariate pattern. One value is stored for each distinct factor/covariate pattern in the data. You can use delta β to detect factor/covariate patterns that have a strong influence on the estimates of the coefficients. This value is based on the Pearson residual.
Formula
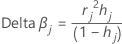
Notation
| Term | Description |
|---|---|
| hj | leverage |
| rj | Pearson residuals |
Leverages
The leverages are the diagonal elements of the generalized hat matrix. The leverages are useful in detecting factor/covariate patterns that may have a significant influence on the results.
Formula
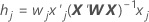
Notation
| Term | Description |
|---|---|
| wj | the jth diagonal element of the weight matrix from fitting the coefficients |
| xj | the jth row of the design matrix |
| X | the design matrix |
| X' | the transpose of X |
| W | the weight matrix from the estimation of the coefficients |
Cook's distance
Formula
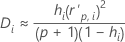
Notation
| Term | Description |
|---|---|
| hi | the leverage for the ith factor/covariate pattern |
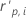 | the standardized Pearson residual for the ith factor/covariate pattern |
| p | the regression degrees of freedom |
DFITS
A measure of the influence of a single deletion on the fitted values. Observations with large DFITS values may be outliers. Minitab calculates an approximate value for DFITS.
Formula

Notation
| Term | Description |
|---|---|
| hi | The leverage for the data point |
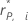 | The deleted Pearson residual for the data point |
Variance inflation factor (VIF)

Notation
| Term | Description |
|---|---|
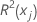 | coefficient of determination with xj as the response variable and the other terms in the model as the predictors |
1. P. McCullagh and J. A. Nelder (1989). Generalized Linear Models, 2nd Edition, Chapman & Hall/CRC, London.
