Find definitions and interpretations for every statistic in the
Regression equation table.
In This Topic
Equations
Use the regression equation to describe the relationship between the response and the terms in the model. The regression equation is an algebraic representation of the model.
The first-order regression equation with a binary response and more than one term takes the following form:

If the model contains curvature, then a polynomial model of higher degree is used. The second-order model is:
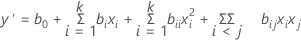
In the regression equation, the letters represent the following:
- y' is the probability of the event, transformed with the link function
- b0 is the constant
- b1, b2, ..., bk are the coefficients
- X1, X2, ..., Xk are the values of the factors
Interpretation
Minitab displays the regression equation in uncoded units unless the model
is nonhierarchical.
For more information on hierarchy, go to
What are hierarchical models?.
Note
When the model is nonhierarchical, the regression equation is in coded units.
- Interpretation of uncoded units
- For a regression equation that is in uncoded units, interpret the coefficients using the natural units of each variable. You can examine the coded coefficients in the Coefficients table. The low level of a categorical factor is -1 and the high level of a categorical factor is +1. Because the equation is averaged over blocks, no coefficients for any blocks are in the equation.
- Interpretation of coded units
- For a regression equation in coded units, the low level of a factor is −1 and the high level of a factor is +1. Because the equation is averaged over blocks, no coefficients for any blocks are in the equation.
