In This Topic
Observed Probability
The observed probability is the number of events divided by the number of trials. For instance, when the number of events is 30 and the number of trials is 495, then the observed probability is 0.06061.
Fit
The fitted value is also called the event probability or predicted probability. Event probability is the chance that the specified experimental event occurs. The event probability estimates the likelihood of an event occurring, such as drawing an ace from a deck of cards or manufacturing a non-conforming part. The probability of an event ranges from 0 (impossible) to 1 (certain).
Interpretation
The experimental response has only two possible values, such as the presence or absence of a particular disease. The event probability is the likelihood that the response for a given factor or covariate pattern occurs (for example, the likelihood that a woman over 50 will develop type-2 diabetes).
Each performance in an experiment is called a trial. For example, if you flip a coin 10 times and record the number of heads, you perform 10 trials of the experiment. If the trials are independent and equally likely, you can estimate the event probability by dividing the number of events by the total number of trials. For example, if you flip 6 heads out of 10 coin tosses, the estimated probability of the event (flipping heads) is:
Number of events ÷ Number of trials = 6 ÷ 10 = 0.6
SE Fit
The standard error of the fit (SE fit) estimates the variation in the event probability for the specified variable settings. The calculation of the confidence interval for the event probability uses the standard error of the fit. Standard errors are always non-negative.
Interpretation
Use the standard error of the fit to measure the precision of the estimate of the event probability. The smaller the standard error, the more precise the predicted mean response.
For example, a researcher studies the factors that affect inclusion in a medical study. For one set of factors, probability that a patient qualifies for inclusion in a study for a new treatment is 0.63, with a standard error of 0.05. For a second set of factors settings, the probability is the same, but with a standard error of the fit of 0.03. The analyst can be more confident that the event probability for the second set of variable settings is close to 0.63.
Confidence interval for fit (95% CI)
These confidence intervals (CI) are ranges of values that are likely to contain the event probability for the population that has the observed values of the predictor variables that are in the model.
Because samples are random, two samples from a population are unlikely to yield identical confidence intervals. But, if you sample many times, a certain percentage of the resulting confidence intervals contain the unknown population parameter. The percentage of these confidence intervals that contain the parameter is the confidence level of the interval.
- Point estimate
- The point estimate is the estimate of the parameter that is calculated from the sample data.
- Margin of error
- The margin of error defines the width of the confidence interval and is affected by the range of the event probabilities, the sample size, and the confidence level.
Interpretation
Use the confidence interval to assess the estimate of the fitted value for the observed values of the variables.
For example, with a 95% confidence level, you can be 95% confident that the confidence interval contains the event probability for the specified values of the variables in the model. The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. If the interval is too wide to be useful, consider increasing your sample size.
Resid
The residual is a measure of how well the observation is predicted by the model. By default, Minitab calculates the deviance residuals. Observations that are poorly fit by the model have high deviance and Pearson residuals. Minitab calculates the residuals for each distinct factor/covariate pattern.
The interpretation of the residual is the same whether you use deviance residuals or Pearson residuals. When the model uses the logit link function, the distribution of the deviance residuals is closer to the distribution of residuals from a least squares regression model. The deviance residuals and the Pearson residuals become more similar as the number of trials for each combination of predictor settings increases.
Interpretation
Plot the residuals to determine whether your model is adequate and meets the assumptions of regression. Examining the residuals can provide useful information about how well the model fits the data. In general, the residuals should be randomly distributed with no obvious patterns and no unusual values. If Minitab determines that your data include unusual observations, it identifies those observations in the Fits and Diagnostics for Unusual Observations table in the output. For more information on unusual values, go to Unusual observations.
Std Resid
The standardized residual equals the value of a residual (ei) divided by an estimate of its standard deviation.
Interpretation
Use the standardized residuals to help you detect outliers. Standardized residuals greater than 2 and less than −2 are usually considered large. The Fits and Diagnostics for Unusual Observations table identifies these observations with an 'R'. When an analysis indicates that there are many unusual observations, the model usually exhibits a significant lack-of-fit. That is, the model does not adequately describe the relationship between the factors and the response variable. For more information, go to Unusual observations.
Standardized residuals are useful because raw residuals might not be good indicators of outliers. The variance of each raw residual can differ by the x-values associated with it. This unequal scale causes it to be difficult to assess the sizes of the raw residuals. Standardizing the residuals solves this problem by converting the different variances to a common scale.
The interpretation of the residual is the same whether you use deviance residuals or Pearson residuals. When the model uses the logit link function, the distribution of the deviance residuals is closer to the distribution of residuals from a least squares regression model. The deviance residuals and the Pearson residuals become more similar as the number of trials for each combination of predictor settings increases.
Del residuals
Each deleted Studentized residual is calculated with a formula that is equivalent to systematically removing each observation from the data set, estimating the regression equation, and determining how well the model predicts the removed observation. Each deleted Studentized residual is also standardized by dividing an observation's deleted residual by an estimate of its standard deviation. The observation is omitted to determine how the model behaves without this observation. If an observation has a large Studentized deleted residual (if its absolute value is greater than 2), it may be an outlier in your data.
Interpretation
Use the deleted Studentized residuals to detect outliers. Each observation is omitted to determine how well the model predicts the response when it is not included in the model fitting process. Deleted Studentized residuals greater than 2 or less than −2 are usually considered large. The observations that Minitab labels do not follow the proposed regression equation well. However, it is expected that you will have some unusual observations. For example, based on the criteria for large residuals, you would expect roughly 5% of your observations to be flagged as having a large residual. If the analysis reveals many unusual observations, the model likely does not adequately describe the relationship between the predictors and the response variable. For more information, go to Unusual observations.
Standardized and deleted residuals may be more useful than raw residuals in identifying outliers. They adjust for possible differences in the variance of the raw residuals due to different values of the predictors or factors.
Hi (leverage)
Hi, also known as leverage, measures the distance from an observation's x-value to the average of the x-values for all observations in a data set.
Interpretation
Hi values fall between 0 and 1. Minitab identifies observations with leverage values greater than 3p/n or .99, whichever is smaller, with an X in the Fits and Diagnostics for Unusual Observations table. In 3p/n, p is the number of coefficients in the model, and n is the number of observations. The observations that Minitab labels with an 'X' may be influential.
Influential observations have a disproportionate effect on the model and can produce misleading results. For example, the inclusion or exclusion of an influential point can change whether a coefficient is statistically significant or not. Influential observations can be leverage points, outliers, or both.
If you see an influential observation, determine whether the observation is a data-entry or measurement error. If the observation is neither a data-entry error nor a measurement error, determine how influential an observation is. First, fit the model with and without the observation. Then, compare the coefficients, p-values, R2, and other model information. If the model changes significantly when you remove the influential observation, examine the model further to determine if you have incorrectly specified the model. You may need to gather more data to resolve the issue.
Cook's distance (D)
Cook's distance (D) measures the effect that an observation has on the set of coefficients in a linear model. Cook's distance considers both the leverage value and the standardized residual of each observation to determine the observation's effect.
Interpretation
Observations with a large D may be considered influential. A commonly used criterion for a large D-value is when D is greater than the median of the F-distribution: F(0.5, p, n-p), where p is the number of model terms, including the constant, and n is the number of observations. Another way to examine the D-values is to compare them to one another using a graph, such as an individual value plot. Observations with large D-values relative to the others may be influential.
Influential observations have a disproportionate effect on the model and can produce misleading results. For example, the inclusion or exclusion of an influential point can change whether a coefficient is statistically significant or not. Influential observations can be leverage points, outliers, or both.
If you see an influential observation, determine whether the observation is a data-entry or measurement error. If the observation is neither a data-entry error nor a measurement error, determine how influential an observation is. First, fit the model with and without the observation. Then, compare the coefficients, p-values, R2, and other model information. If the model changes significantly when you remove the influential observation, examine the model further to determine if you have incorrectly specified the model. You may need to gather more data to resolve the issue.
DFITS
DFITS measures the effect each observation has on the fitted values in a linear model. DFITS represents approximately the number of standard deviations that the fitted value changes when each observation is removed from the data set and the model is refit.
Interpretation
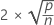
| Term | Description |
|---|---|
| p | the number of model terms |
| n | the number of observations |
If you see an influential observation, determine whether the observation is a data-entry or measurement error. If the observation is neither a data-entry error nor a measurement error, determine how influential an observation is. First, fit the model with and without the observation. Then, compare the coefficients, p-values, R2, and other model information. If the model changes significantly when you remove the influential observation, examine the model further to determine if you have incorrectly specified the model. You may need to gather more data to resolve the issue.
