In This Topic
Factors
The number shows how many factors are in the design.
Interpretation
The factors are the variables that you control in the experiment. Factors are also known as independent variables, explanatory variables, and predictor variables. Factors assume only a limited number of possible values, known as factor levels. Factors can have text or numeric levels. For numeric factors, you select specific levels for the experiment, even though many values for the factor are possible.
For example, a chemist is studying how to maximize crystal growth. The chemist wants to study three continuous variables (time, temperature, and percentage of the catalyst in the air inside the chamber) and one categorical factor (additive).
In a response surface design, you designate a low level and a high level for each continuous factor. These factor levels define the "cube" around which the design is built. The "cube" is often centered around the current operating conditions for the process. For a central composite design, you may have design points in the "cube," on the "cube," or outside the "cube."
Base and total runs
The number of base runs is the number of factor level combinations in the base design. The total number of runs is the number of base runs times the number of replicates.
Interpretation
| Run | Factor 1 | Factor 2 | Response |
|---|---|---|---|
| 1 | −1 | −1 | 11 |
| 2 | 1 | −1 | 12 |
| 3 | −1 | 1 | 10 |
| 4 | 1 | 1 | 9 |
Note
When you conduct an experiment, the run order should be randomized.
Each run corresponds to a design point, and the entire set of runs is the design. Multiple executions of the same experimental conditions are considered separate runs and are called replicates.
Base and total blocks
Blocks are a group of homogenous experimental units (observations). Base blocks are the number of blocks before replicates are added to the design. Total blocks include any blocks created by replicates in your design.
Although every observation should be taken under identical experimental conditions (other than those that are being varied as part of the experiment), this is not always possible. Nuisance factors that can be classified can be eliminated using a blocked design. For example, an experiment may be carried out over several days with large variations in temperature and humidity, or data may be collected in different plants, or by different technicians. Observations collected under the same experimental conditions are said to be in the same block.
Replicates
The number shows how many replicates are in the design.
Interpretation
Replicates are multiple experimental runs with the same factor level settings (levels). One replicate is equivalent to the base design, where you conduct each factor level combination once. With two replicates, you perform each factor level combination in the base design twice (in random order), and so on.
For example, if you have 3 factors with 2 levels each and you test all combinations of factor levels (full factorial design), the base design represents 1 replicate and has 8 runs (23). If you add 2 replicates, the design includes 3 replicates and has 24 runs.
- If you are trying to create a prediction model, multiple replicates can increase the precision of your model.
- If you include replicates, you might be able to detect smaller effects or have greater power to detect an effect of fixed size.
- Screening designs (2-level factorial designs), which are used to reduce a large set of factors, usually don't include replicates.
- Your resources can dictate the number of replicates you can run. For example, if your experiment is extremely costly, you might be able to run the base design only one time.
For information on the difference between replicates and repeats, go to Replicates and repeats in designed experiments.
Alpha
Alpha (α) determines the distance of each axial point (also called star point) from the center in a central composite design.
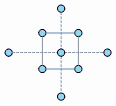
A value less than one puts the axial points in the cube; a value equal to one puts them on the faces of the cube; and a value greater than one puts them outside the cube.
Alpha, along with the number of center points, determines whether a design can be orthogonally blocked and whether it is rotatable. Orthogonally blocked designs allow model terms and block effects to be estimated independently and minimize the variance in the regression coefficients. Rotatable designs produce a constant prediction variance at all points that are equidistant from the design center.
When the design includes blocks and you cannot achieve both properties at the same time, the default designs use α such that the design includes orthogonal blocks. When there are no blocks, the default designs use α such that the design is rotatable.
Minitab's alpha values agree with those listed in Montgomery1.
Cube points, center points in a cube, and axial points
A central composite design consists of a "cube" portion made up of the design points from a 2K factorial or 2k−p fractional factorial design; 2K axial or "star" points, and center points (where K is the number of factors).
Interpretation

Center points in axial
Design points in which all factors are set at their center level simultaneously and are in axial blocks. An axial block is a block that contains axial points rather than cube points.
Interpretation
- Factor A has low and high levels: 20 and 30
- Factor B has low and high levels: 150 and 200.
The center point for this design is located where Factor A is equal to 25 and Factor B is equal to 175.
Design table
The design table shows the factor settings for each experimental run. Because the design table takes up less space than the worksheet, it can be useful for reports with limited space.
- −1 indicates the low factor level.
- 1 indicates the high level.
- 0 indicates the middle point between the low and high level.
- The negative and positive default α-values indicate the low and high axial levels.
For categorical factors, Minitab represents the factor settings with numbers that correspond to the categories.
Interpretation
Use the design table to see the factor settings for each run and the order of the runs in the design. In these results, the design table shows 14 runs in each of two blocks, for a total of 28 runs. The runs are randomized within each block. −1.414 and 1.414 indicate the low and high axial levels. In the first run, the continuous factors A and B are at the middle point between the high and low level and the categorical factor C is at level 1.
Design Table (randomized)
| Run | Blk | A | B | C |
|---|---|---|---|---|
| 1 | 1 | 0.00000 | 0.00000 | 1 |
| 2 | 1 | -1.00000 | -1.00000 | 1 |
| 3 | 1 | 1.00000 | -1.00000 | 1 |
| 4 | 1 | 0.00000 | 0.00000 | 1 |
| 5 | 1 | -1.00000 | -1.00000 | 2 |
| 6 | 1 | 0.00000 | 0.00000 | 1 |
| 7 | 1 | -1.00000 | 1.00000 | 1 |
| 8 | 1 | 1.00000 | 1.00000 | 2 |
| 9 | 1 | 1.00000 | 1.00000 | 1 |
| 10 | 1 | -1.00000 | 1.00000 | 2 |
| 11 | 1 | 0.00000 | 0.00000 | 2 |
| 12 | 1 | 0.00000 | 0.00000 | 2 |
| 13 | 1 | 0.00000 | 0.00000 | 2 |
| 14 | 1 | 1.00000 | -1.00000 | 2 |
| 15 | 2 | 0.00000 | 0.00000 | 2 |
| 16 | 2 | 0.00000 | 0.00000 | 1 |
| 17 | 2 | 0.00000 | 1.41421 | 2 |
| 18 | 2 | -1.41421 | 0.00000 | 1 |
| 19 | 2 | -1.41421 | 0.00000 | 2 |
| 20 | 2 | 0.00000 | 0.00000 | 2 |
| 21 | 2 | 0.00000 | -1.41421 | 2 |
| 22 | 2 | 0.00000 | 0.00000 | 1 |
| 23 | 2 | 0.00000 | -1.41421 | 1 |
| 24 | 2 | 1.41421 | 0.00000 | 2 |
| 25 | 2 | 0.00000 | 0.00000 | 2 |
| 26 | 2 | 0.00000 | 0.00000 | 1 |
| 27 | 2 | 0.00000 | 1.41421 | 1 |
| 28 | 2 | 1.41421 | 0.00000 | 1 |
