In This Topic
Histogram of residuals
The histogram of the residuals shows the distribution of the residuals for all observations.
Interpretation
| Pattern | What the pattern may indicate |
|---|---|
| A long tail in one direction | Skewness |
| A bar that is far away from the other bars | An outlier |
Because the appearance of a histogram depends on the number of intervals used to group the data, don't use a histogram to assess the normality of the residuals.
A histogram is most effective when you have approximately 20 or more data points. If the sample is too small, then each bar on the histogram does not contain enough data points to reliably show skewness or outliers.
Residuals versus fits
The residuals versus fits graph plots the residuals on the y-axis and the fitted values on the x-axis.
Interpretation
Use the residuals versus fits plot to verify the assumption that the residuals are randomly distributed and have constant variance. Ideally, the points should fall randomly on both sides of 0, with no recognizable patterns in the points.
| Pattern | What the pattern may indicate |
|---|---|
| Fanning or uneven spreading of residuals across fitted values | Nonconstant variance |
| Curvilinear | A missing higher-order term |
| A point that is far away from zero | An outlier |
| A point that is far away from the other points in the x-direction | An influential point |

Plot with outlier
One of the points is much larger than all of the other points. Therefore, the point is an outlier. If there are too many outliers, the model may not be acceptable. You should try to identify the cause of any outlier. Correct any data entry or measurement errors. Consider removing data values that are associated with abnormal, one-time events (special causes). Then, repeat the analysis.
Plot with nonconstant variance
The variance of the residuals increases with the fitted values. Notice that, as the value of the fits increases, the scatter among the residuals widens. This pattern indicates that the variances of the residuals are unequal (nonconstant).
- Verify that the observation is not a measurement error or data-entry error.
- Consider performing the analysis without this observation to determine how it impacts your results.
Residuals versus order
The residuals versus order plot displays the residuals in the order that the data were collected.
Interpretation
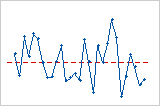
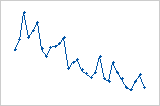
Trend
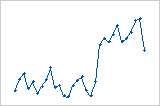
Shift
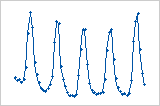
Cycle
Residuals versus variables
The residuals versus variables plot displays the residuals versus another variable. The variable could already be included in your model. Or, the variable may not be in the model, but you suspect it affects the response variable.
Interpretation
If the variable is already included in the model, use the plot to determine whether you should add a higher-order term of the variable. If the variable is not already included in the model, use the plot to determine whether the variable is affecting the response in a systematic way.
| Pattern | What the pattern may indicate |
|---|---|
| Pattern in residuals | The variable affects the response in a systematic way. If the variable is not in your model, include a term for that variable and refit the model. |
| Curvature in the points | A higher-order term of the variable should be included in the model. For example, a curved pattern indicates that you should add a squared term. |
