The confidence levels associated with the confidence intervals often used in multiple comparisons to identify significant differences between specific factor levels in an ANOVA. These confidence levels are analogous to the individual and family error rates but applied to confidence intervals.
What is an individual confidence level?
The percentage of confidence intervals that will include the true population parameter or true difference between factor levels if the study were repeated multiple times.
What is a simultaneous confidence level?
The percentage of times that a group of confidence intervals will all include the true population parameters or true differences between factor levels if the study were repeated multiple times. The simultaneous confidence level is based on both the individual confidence level and the number of confidence intervals. For a single comparison, the simultaneous confidence level is equal to the individual confidence level. However, each additional confidence interval causes the simultaneous confidence level to decrease in a cumulative way.
It is important to consider the simultaneous confidence level when you examine multiple confidence intervals because your chances of excluding a parameter or true difference between factor levels for a family of confidence intervals is greater than for any one confidence interval.
Tukey's method, Fisher's least significant difference (LSD), Hsu's multiple comparisons with the best (MCB), and Bonferroni confidence intervals are methods for calculating and controlling the individual and simultaneous confidence levels.
Example of individual confidence intervals and simultaneous confidence intervals
For example, you measure the response times for memory chips. You take a sample of 25 chips from five different manufacturers.
You decide to examine all 10 comparisons between the five plants to determine specifically which means are different. Using Tukey's method, you specify that the entire set of confidence intervals should have a 95% simultaneous confidence level. Minitab calculates that the 10 individual confidence levels need to be 99.35% to obtain the 95% simultaneous confidence level. These wider Tukey confidence intervals provide less precise estimates of the population parameters but limit the probability that one or more of the confidence intervals does not contain the true difference to a maximum of 5%. Understanding this context, you can then examine the confidence intervals to determine whether any do not include zero, which would denote a significant difference.
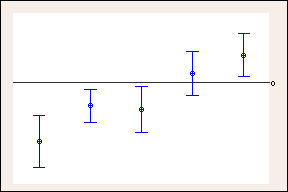
Confidence intervals with 95% individual confidence levels
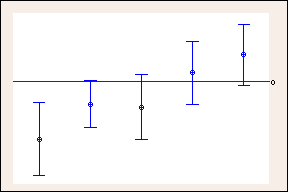
Confidence intervals with 99.35% individual confidence levels to obtain a 95% simultaneous confidence level using Tukey's
Comparison of 95% confidence intervals to the wider 99.35% confidence intervals used by Tukey's in the previous example. The reference line at 0 shows how the wider Tukey confidence intervals can change your conclusions. Confidence intervals that contain zero denote no difference. (Only 5 of the 10 comparisons are shown because of space considerations.)
