Notation
| Term | Description |
|---|---|
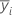 | the sample mean for the ith factor level |
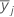 | the sample mean jth factor level |
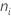 | the number of observations in level i |
| r | the number of levels |
| s | the pooled standard deviation or sqrt(MSE) |
| u | the degrees of freedom for error |
| α | the simultaneous probability of making a Type I error |
| α* | the individual probability of making a Type I error |
Tukey:
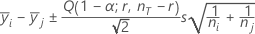
where Q = upper α percentile of the studentized range distribution with r and nT - r degrees of freedom.
To find the individual error rate from the simultaneous error rate, use the following formula:

Fisher:
where t = upper α/2 point of the Student's t-distribution with u df.
To find the simultaneous confidence level from the individual error rate, use the following formula:
Dunnett:

To see how d is calculated, refer to page 63 in Hsu1.
Hsu's MCB:
We give formulas for the case where all group sizes are equal to n. Formulas for unequal group sizes are found in Hsu1. Suppose you chose the best to be the largest mean, and you want the confidence interval for the ith mean minus the largest of the others.
The lower endpoint is the smaller of zero and

The upper endpoint is the larger of zero and

To see how d is calculated, refer to page 83 in Hsu1.
When the best is the smallest of the level means, the formulas are the same, except that max is replaced by min.
Games-Howell and Welch Test
The Welch test statistic is computed as follows.
The p-value for the Welch test is an upper tail probability for an F distribution with numerator degrees of freedom k - 1, where k is the number of X levels, and denominator degrees of freedom given by:
The comparison interval for μi - μj is
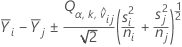
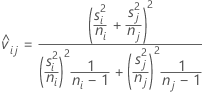
The T-ratio used to compute the adjusted P-value equals:
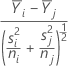
Where:
The jth response in the ith level of the categorical factor equals:Yij, j = 1, ... , ni; i = 1, ... k
The average response at the ith level equals:
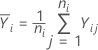
The sample variance equals:
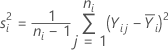
The weight for level i equals:
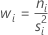
The sum of all weights equals:
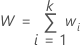
The overall weighted average of responses equals:
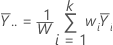
Acknowledgment
We are very grateful for assistance in the design and implementation of multiple comparisons from Jason C. Hsu.
[1] J.C. Hsu (1996). Multiple Comparisons, Theory and methods. Chapman & Hall.
