In This Topic
Estimation method
You can select either Restricted maximum likelihood (REML) or Maximum likelihood (ML). Usually, you use Restricted maximum likelihood (REML) because the variance component estimator by REML is approximately unbiased, while the ML estimator is biased. However, the bias gets smaller for larger sample sizes.
Use Maximum likelihood (ML) if you need to test whether a nested model with a fewer number of fixed effect terms is as good as its corresponding reference model that has more fixed effect terms, given both models have the same number of random terms and error variance structure. Specifically, let  be the negative 2 log likelihood from the full model, and
be the negative 2 log likelihood from the full model, and  be the negative 2 log likelihood from the smaller model.
be the negative 2 log likelihood from the smaller model.
Under the null hypothesis, asymptotically, 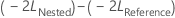 follows a chi- square distribution with degrees of freedom equal to the difference in the number of parameters for fixed effect terms between the reference model and the nested model. You can use the likelihood ratio test to evaluate whether a subset of fixed effect terms can be removed from the reference model.
follows a chi- square distribution with degrees of freedom equal to the difference in the number of parameters for fixed effect terms between the reference model and the nested model. You can use the likelihood ratio test to evaluate whether a subset of fixed effect terms can be removed from the reference model.
For more information on the likelihood ratio test of fixed parameters in a mixed effects model, see B. T. West, K.B. Welch, and A.T. Gałecki (2007). Linear Mixed Models: A Practical Guide Using Statistical Software, First Edition. Chapman and Hall/CRC (34–36).
Test method for fixed effects
Usually, you use Kenward-Roger approximation because the calculations include an adjustment that reduces bias from small sample sizes. You can also use Satterthwaite approximation. In general, the larger the sample size, the less difference between the two methods.
Weights
In Weights, enter a numeric column of weights for all response values. Use Weights if the variance of the random error inside the response values is not constant. Instead, for each response value, the variance equals the inverse of the corresponding weight multiplying by a constant.
The weights must be greater than or equal to zero. The weights column must have the same number of rows as the response column.
Confidence level for all intervals
Enter the level of confidence for all the confidence intervals in the output.
Usually, a confidence level of 95% works well. A 95% confidence level indicates that, if you took 100 random samples from the population for a parameter of interest, the confidence intervals for approximately 95 of the samples would contain the true value of the unknown parameter. For a given set of data, a lower confidence level produces a narrower interval, and a higher confidence level produces a wider interval.
Note
To display the confidence intervals, you must go to the Results sub-dialog box, and from Display of results, select Expanded tables.
Type of confidence interval
You can select a two-sided interval or a one-sided bound. For the same confidence level, a bound is closer to the point estimate than the interval. The upper bound does not provide a likely lower value. The lower bound does not provide a likely upper value.
- Two-sided
-
- Use a two-sided confidence interval to estimate both likely lower and upper values for the parameter of interest.
- Lower bound
-
- Use a lower confidence bound to estimate a likely lower value for the parameter of interest.
- Upper bound
-
- Use an upper confidence bound to estimate a likely higher value for the parameter of interest.
Means
You can display the fitted means for the main effects, the two-way interactions, or all terms in the model in the output. Alternatively, you can display the means for a subset of these terms, or no terms.
If you select Specified terms, use the I = Calculate means for term for term button to identify the terms. Select a term in the list, then press the button. An I indicates that the mean of the term will be displayed. If a term you expected to see in the list does not appear, you need to add it to the model.
