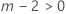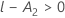In This Topic
Tests of fixed effect terms
The tests of the fixed effect terms are F tests. The null hypothesis for the test depends on whether the test is for a fixed factor term or a covariate term. For a fixed factor term, the null hypothesis is that the term does not significantly affect the response. For a covariate term, the null hypothesis is that no association exists between the response and the covariate term.
Minitab offers 2 methods to test fixed effect terms: Kenward-Roger approximation and Satterthwaite approximation. For more information on Kenward-Roger approximation, see Kenward and Roger.1 For more information on Satterthwaite approximation, see Giesbrecht and Burns 2 as well as Fai and Cornelius. 3
The calculation of the denominator degrees of freedom for the F-statistic and the calculation of the F-statistic differ. The calculation of the numerator degrees of freedom and the determination of a p-value for a given F-statistic are the same for both methods.
Kenward-Roger approximation
Kenward-Roger approximation is one method to test the statistical significance of fixed effect terms.
F-statistic
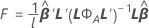
where
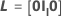
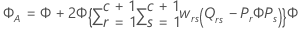
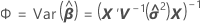
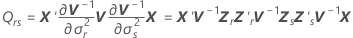
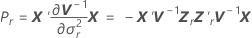
Notation
| Term | Description |
|---|---|
| l | the numerator degrees of freedom, which is the number of parameters in the term to test |
| 0 | the matrix with 0 components |
| Il | the identity matrix with l dimension |
| c + 1 | the number of variance components |
| wrs | (r, s)th component of the asymptotic variance-covariance matrix of 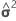 |
| V−1 | the inverse of the variance-covariance matrix |
For further details on the notation, go to the Methods section.
Denominator degrees of freedom

where
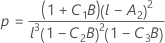

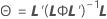
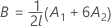

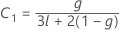
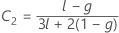
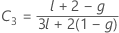
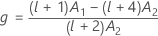
Kenward and Roger λ
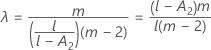
If either condition is not true, then λ = 1.
Under the null hypothesis, lambda × F is asymptotically F distributed with degrees of freedom DF Num, and DF Den. The calculation of the P-value uses this property.
Satterthwaite approximation
Satterthwaite approximation is one method to test the statistical significance of fixed effect terms.
F-statistic
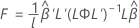
where L and  have the same definitions as in Kenward-Roger approximation.
have the same definitions as in Kenward-Roger approximation.
Denominator degrees of freedom
The process for the determination of the degrees of freedom has multiple steps.
-
Perform the spectral decomposition on the variance of the fixed effect parameter vector estimate:

where P is an orthogonal matrix of eigenvectors and D is a diagonal matrix of eigenvalues, both of dimension l × l.
-
Define lr to be the rth row of P'L, r = 1, ..., l and let
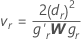 where dr is the rth diagonal element of D, W is the asymptotic variance covariance matrix of
where dr is the rth diagonal element of D, W is the asymptotic variance covariance matrix of and gr is the gradient vector of the following elements:
and gr is the gradient vector of the following elements:
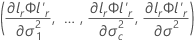
where
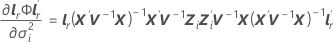
i = 1, …, c, and
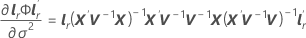
-
Let
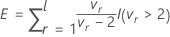
where
 is an indicator function that eliminates terms with
is an indicator function that eliminates terms with 
-
The denominator degrees of freedom depend on the value of E.
- If E > l then the degrees of freedom follow:

- Otherwise, DF Den = 1
- If E > l then the degrees of freedom follow:
Numerator degrees of freedom (DF Num)
| Effect | DF |
|---|---|
| Fixed Factor |  |
| Covariate | 1 |
| Interactions that involve fixed factors | 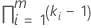 |
Notation
| Term | Description |
|---|---|
| k | the number of levels in the fixed factor term |
| m | the number of factors in the interaction |
P-value – Tests of fixed effects

Notation
| Term | Description |
|---|---|
 | the cumulative distribution function of the F-distribution with degrees of freedom equal to DF Num and DF Den, respectively |
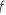 | the calculated F-value for a term |