- Variance estimation
-
Usually, you use Restricted maximum likelihood (REML) because the variance component estimator from REML is approximately unbiased, while the maximum likelihood estimator is biased. However, the bias gets smaller for larger sample sizes.
Use Maximum likelihood (ML) if you need to test whether a nested model with a fewer number of fixed effect terms is as good as its corresponding reference model that has more fixed effect terms, given both models have the same number of random terms and error variance structure. Specifically, let
 be the negative 2 log likelihood from the full model, and
be the negative 2 log likelihood from the full model, and  be the negative 2 log likelihood from the smaller model.
be the negative 2 log likelihood from the smaller model. Under the null hypothesis, asymptotically,
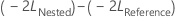 follows a chi- square distribution with degrees of freedom equal to the difference in the number of parameters for fixed effect terms between the reference model and the nested model. You can use the likelihood ratio test to evaluate whether a subset of fixed effect terms can be removed from the reference model.
follows a chi- square distribution with degrees of freedom equal to the difference in the number of parameters for fixed effect terms between the reference model and the nested model. You can use the likelihood ratio test to evaluate whether a subset of fixed effect terms can be removed from the reference model. For more information on the likelihood ratio test of fixed parameters in a mixed effects model, see West, Welch, and Galecki.1
- DF for fixed effects
-
Usually, you use Kenward-Roger approximation because the calculations use an adjusted estimator of the covariance matrix for the response values that reduces small sample bias. You can also use Satterthwaite approximation. In general, the larger the sample size, the less difference between the two methods.
