Means
The means table displays the fitted means of the observations within groups based on one or more categorical variables. Fitted means use least squares to predict the mean response values of a balanced design.
Interpretation
The fitted means estimate the average response at different levels of one factor while averaging over the levels of the other factors.
Use the Means table to understand the statistically significant differences between the factor levels in your data. The mean of each group provides an estimate of each population mean. Look for differences between group means for terms that are statistically significant.
For main effects, the table displays the groups within each factor and their means. For interaction effects, the table displays all possible combinations of the groups. If an interaction term is statistically significant, do not interpret the main effects without considering the interaction effects.
In these results, the Means table shows how the mean usability and quality ratings varies by method, plant, and the method*plant interaction. Method and the interaction term are statistically significant at the 0.10 level. The table shows that method 1 and method 2 are associated with mean usability ratings of 4.819 and 6.212 respectively. The difference between these means is larger than the difference between the corresponding means for quality rating. This confirms the interpretation of the eigen analysis.
However, because the Method*Plant interaction term is also statistically significant, do not interpret the main effects without considering the interaction effects. For example, the table for the interaction term shows that with method 1, plant C is associated with the highest usability rating and the lowest quality rating. However, with method 2, plant A is associated with the highest usability rating and a quality rating that is nearly equal to the highest quality rating.
Least Squares Means for Responses
| Usability Rating | Quality Rating | |||
|---|---|---|---|---|
| Mean | SE Mean | Mean | SE Mean | |
| Method | ||||
| Method 1 | 4.819 | 0.165 | 5.242 | 0.193 |
| Method 2 | 6.212 | 0.179 | 6.026 | 0.211 |
| Plant | ||||
| Plant A | 5.708 | 0.192 | 5.833 | 0.226 |
| Plant B | 5.493 | 0.232 | 5.914 | 0.273 |
| Plant C | 5.345 | 0.206 | 5.155 | 0.242 |
| Method*Plant | ||||
| Method 1 Plant A | 4.667 | 0.272 | 5.417 | 0.319 |
| Method 1 Plant B | 4.700 | 0.298 | 5.400 | 0.350 |
| Method 1 Plant C | 5.091 | 0.284 | 4.909 | 0.334 |
| Method 2 Plant A | 6.750 | 0.272 | 6.250 | 0.319 |
| Method 2 Plant B | 6.286 | 0.356 | 6.429 | 0.418 |
| Method 2 Plant C | 5.600 | 0.298 | 5.400 | 0.350 |
SE Mean
The standard error of the mean (SE Mean) estimates the variability between fitted means that you would obtain if you took samples from the same population again and again.
For example, you have a mean delivery time of 3.80 days, with a standard deviation of 1.43 days, from a random sample of 312 delivery times. These numbers yield a standard error of the mean of 0.08 days (1.43 divided by the square root of 312). If you took multiple random samples of the same size, from the same population, the standard deviation of those different sample means would be around 0.08 days.
Interpretation
Use the standard error of the mean to determine how precisely the fitted mean estimates the population mean.
A smaller value of the standard error of the mean indicates a more precise estimate of the population mean. Usually, a larger standard deviation results in a larger standard error of the mean and a less precise estimate of the population mean. A larger sample size results in a smaller standard error of the mean and a more precise estimate of the population mean.
Mean (covariate)
The mean of the covariate is the average of the data, which is the sum of all the observations divided by the number of observations. The mean summarizes the sample values with a single value that represents the center of the data.
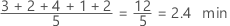
Interpretation
Use the mean to describe the covariate with a single value that represents the center of the data.
Standard Deviation (StDev)
The standard deviation is the most common measure of dispersion, or how spread out the data are around the mean. The symbol σ (sigma) is often used to represent the standard deviation of a population. The symbol s is used to represent the standard deviation of a sample.
Interpretation
- Approximately 68% of the values fall within one standard deviation of the mean.
- 95% of the values fall within two standard deviations.
- 99.7% of the values fall within three standard deviations.
The sample standard deviation of a group is an estimate of the population standard deviation of that group. The standard deviations are used to calculate the confidence intervals and the p-values. Larger sample standard deviations result in less precise (wider) confidence intervals and lower statistical power.
Analysis of variance assumes that the population standard deviations for all levels are equal. If you cannot assume equal variances, use Welch's ANOVA, which is an option for One-Way ANOVA that is available in Minitab Statistical Software.
