Minitab®  Support

Methods and formulas for Balanced ANOVA

Learn more about
Select the method or formula of your choice.

In This Topic

Balanced ANOVA model

The balanced ANOVA model for three or more factors is a straightforward extension of a two-way analysis of variance model.

A three-factor balanced ANOVA model with factors A, B, and C is:

yijkm = μ + α i+ β j + γ k + (αβ)ij+ (αγ)ik+ (βγ)jk+ (αβγ)ijk+εijkm

If the factors are fixed, Σαi = 0, Σβj = 0, Σγk = 0, Σ(αβ)ij = 0, Σ(αγ)ik = 0, Σ(βγ)jk = 0, Σ(αβγ)ijk = 0 and εijkm are independent N(0, σ2).

If the factors are random, α i, β j , γk, (αβ)ij, (αγ)ik, (βγ)jk, (αβγ)ijk,and εijkmare independent random variables. The variables are normally distributed with mean zero and variances given by V(αi) = σ2α,V(β j) = σ2β,V(γk) = σ2γ, V[(αβ)ij] = σ2αβ, V[(αγ)jk] = σ2αγ, V[(βγ)jk] = σ2βγ, V(εijkm) = σ2.

The three-factor model can be extended to models with more than three factors.

Factor means

Formula

The average of the observations for a factor at a given level. The formulas are:

Mean of Factor A: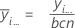

Mean of Factor B:

Mean of Factor C: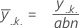

Overall mean:

Notation

TermDescription
yi...sum of all observations for the ith factor level of A
y.j..sum of all observations for the jth factor level of B
y..k.sum of all observations for the kth factor level of C
y....sum of all observations in the sample
anumber of levels in A
bnumber of levels in B
cnumber of levels in C
nnumber of observations in each combination of the factor and levels

Sum of squares (SS)

The sum of squared distances. SS Total is the total variation in the data. SS (A), SS (B), and SS (C) represent the amount of variation of estimated factor level mean around the overall mean. They are also known as the sum of squares between treatments. SS(AB), SS(AC), SS(BC) and SS(ABC) represent the amount of variation explained by each respective interaction term. SS Error represents the amount of variation between the fitted value and the actual observation. It is also known as error within treatments. These formulas assume a full model is fit. The calculations are:

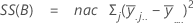
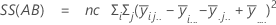
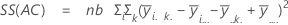
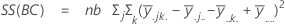
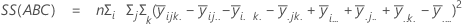
  • SS Error = SS Total - SS (for all terms in model)

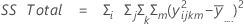
Notation

TermDescription
anumber of levels in factor A
bnumber of levels in factor B
cnumber of levels in factor C
ntotal number of trials
mean of the ith factor level of factor A
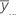overall mean of all observations
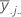mean of the jth factor level of factor B
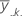mean of the kth factor level of factor C
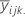estimated treatment mean

Degrees of Freedom (DF)

The degrees of freedom for each component of the model are:

Sources of variation DF
Factor ki – 1
Covariates and interactions between covariates 1
Interactions that involve factors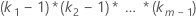
Regression p
Error n – p – 1
Total n – 1

Notation

TermDescription
kinumber of levels in the ith factor
mnumber of factors
n number of observations
p number of coefficients in the model, not counting the constant

Mean square (MS)

Formulas

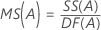
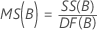
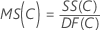
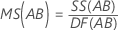
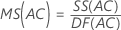
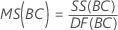
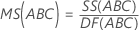
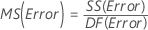
F

For a 3-factor ANOVA with all fixed factors, these formulas are the F-statistics when the model is full.

Formulas

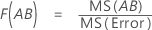
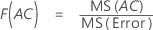
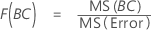
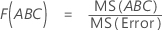
  • For F(A), the degrees of freedom for the numerator are a - 1 and for the denominator are (n - 1)abc.
  • For F(B), the degrees of freedom for the numerator are b - 1 and for the denominator are (n - 1)abc.
  • For F(C), the degrees of freedom for the numerator are c - 1 and for the denominator are (n - 1)abc.
  • For F(AB), the degrees of freedom for the numerator are (a - 1)(b - 1) and for the denominator are (n - 1)abc.
  • For F(AC), the degrees of freedom for the numerator are (a - 1)(c - 1) and for the denominator are (n - 1)abc.
  • For F(BC), the degrees of freedom for the numerator are (b - 1)(c - 1) and for the denominator are (n - 1)abc.
  • For F(ABC), the degrees of freedom for the numerator are (a - 1)(b - 1)(c - 1) and for the denominator are (n - 1)abc.

If there are random factors in the model, the F ratio for each term is determine by the expected mean square for each term.

Larger values of F support rejecting the null hypothesis. You can conclude that the effect is statistically significant.

P-value – Analysis of variance table

The p-value is a probability that is calculated from an F-distribution with the degrees of freedom (DF) as follows:

Numerator DF
sum of the degrees of freedom for the term or the terms in the test
Denominator DF
degrees of freedom for error

Formula

1 − P(F ≤ fj)

Notation

TermDescription
P(F ≤ f)cumulative distribution function for the F-distribution
ff-statistic for the test

S

Notation

TermDescription
MSEmean square error

R-sq

R2 is also known as the coefficient of determination.

Formula

Notation

TermDescription
yi i th observed response value
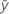mean response
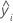i th fitted response

R-sq (adj)

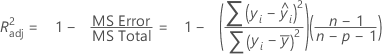
While the calculations for adjusted R2 can produce negative values, Minitab displays zero for these cases.

Notation

TermDescription
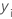ith observed response value
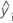ith fitted response
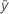mean response
nnumber of observations
pnumber of terms in the model

Variance components

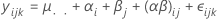
Minitab calculates variance components only for random factors. A model with two random factors is used to present the formulas.

where, αi, βj , (αβ)ij, and εijk are independent random variables. The variables are normally distributed with mean zero and variances given by these formulas:

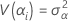
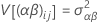
These variances are the variance components. In this case, test the hypothesis that the variance components are equal to zero.

For a restricted mixed model with two factors, the model is:

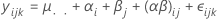
where αi is a fixed effect and βj is a random effect, (αβ)ij, is a random effect, and εijk is random error. The Σαi = 0 and Σ(αβ)ij = 0 for each j. The variances are V(βj) = σ2β,V[(αβ)ij] =[(a - 1)/a]σ2αβ, and V(εijk) = σ2. σ2β, σ2αβ, and σ2 are variance components. Summing the interaction component over the fixed factor equals zero, which indicates this is the restricted mixed model.

For an unrestricted mixed model with a fixed factor, A, and a random factor, B, this formula describes the model:

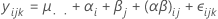
where αi are fixed effects and βj, (αβ)ij and εijk are uncorrelated random variables having zero means and these variances:

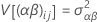
These variances are the variance components. The Σα i = 0 and Σ(αβ)ij = 0 for each j.

This information is for balanced models. For information on unbalanced or more complex models, see Montgomery1 and Neter2.

  1. D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
  2. J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

Expected mean squares

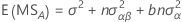
The formulas for the expected mean squares for a random effects model with two factors, A and B are:

The formulas for the expected mean squares for a restricted mixed model with two factors, A (fixed) and B (random) are:

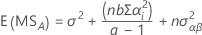
The formulas for the expected mean squares for an unrestricted mixed model with a fixed factor, A, and a random factor, B, are:

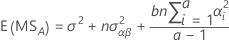
For the general rules on calculating expected mean squares, and for information on unbalanced or more complex models, see Montgomery1 and Neter2.

  1. D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
  2. J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

Notation

TermDescription
bnumber of levels in factor B
anumber of levels in factor A
nnumber of observations
σ2estimated variance of the model
estimated variance of A
estimated variance of B
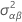estimated variance of AB
fixed effects of A

F-statistic for models with random factors

How the F-statistics in the ANOVA output are calculated

Each F-statistic is a ratio of mean squares. The numerator is the mean square for the term. The denominator is chosen such that the expected value of the numerator mean square differs from the expected value of the denominator mean square only by the effect of interest. The effect for a random term is represented by the variance component of the term. The effect for a fixed term is represented by the sum of squares of the model components associated with that term divided by its degrees of freedom. Therefore, a high F-statistic indicates a significant effect.

When all the terms in the model are fixed, the denominator for each F-statistic is the mean square of the error (MSE). However, for models that include random terms, the MSE is not always the correct mean square. The expected mean squares (EMS) can be used to determine which is appropriate for the denominator.

Example

Suppose you performed an ANOVA with the fixed factor Screen and the random factor Tech, and get the following output for the EMS:
Source Expected Mean Square for Each Term
(1) Screen (4) + 2.0000(3) + Q[1]
(2) Tech (4) + 2.0000(3) + 4.0000(2)
(3) Screen*Tech (4) + 2.0000(3)
(4) Error (4)

A number with parentheses indicates a random effect associated with the term listed beside the source number. (2) represents the random effect of Tech, (3) represents the random effect of the Screen*Tech interaction, and (4) represents the random effect of Error. The EMS for Error is the effect of the error term. In addition, the EMS for Screen*Tech is the effect of the error term plus two times the effect of the Screen*Tech interaction.

To calculate the F-statistic for Screen*Tech, the mean square for Screen*Tech is divided by the mean square of the error so that the expected value of the numerator (EMS for Screen*Tech = (4) + 2.0000(3)) differs from the expected value of the denominator (EMS for Error = (4)) only by the effect of the interaction (2.0000(3)). Therefore, a high F-statistic indicates a significant Screen*Tech interaction.

A number with Q[ ] indicates the fixed effect associated with the term listed beside the source number. For example, Q[1] is the fixed effect of Screen. The EMS for Screen is the effect of the error term plus two times the effect of the Screen*Tech interaction plus a constant times the effect of Screen. Q[1] equals (b*n * sum((coefficients for levels of Screen)**2)) divided by (a - 1), where a and b are the number of levels of Screen and Tech, respectively, and n is the number of replicates.

To calculate the F-statistic for Screen, the mean square for Screen is divided by the mean square for Screen*Tech so that the expected value of the numerator (EMS for Screen = (4) + 2.0000(3) + Q[1] ) differs from the expected value of the denominator (EMS for Screen*Tech = (4) + 2.0000(3) ) only by the effect due to the Screen (Q[1]). Therefore, a high F-statistic indicates a significant Screen effect.

Why does my ANOVA output include an "x" beside a p-value in the ANOVA table and the label "Not an exact F-test"?

An exact F-test for a term is one in which the expected value of the numerator mean squares differs from the expected value of the denominator mean squares only by the variance component or the fixed factor of interest.

Sometimes, however, such a mean square cannot be calculated. In this case, Minitab uses a mean square that results in an approximate F-test and displays an "x" beside the p-value to identify that the F-test is not exact.

For example, suppose you performed an ANOVA with the fixed factor Supplement and the random factor Lake, and the got following output for the expected mean squares (EMS):
Source Expected Mean Square for Each Term
(1) Supplement (4) + 1.7500(3) + Q[1]
(2) Lake (4) + 1.7143(3) + 5.1429(2)
(3) Supplement*Lake (4) + 1.7500(3)
(4) Error (4)

The F-statistic for Supplement is the mean square for Supplement divided by the mean square for the Supplement*Lake interaction. If the effect for Supplement is very small, the expected value of the numerator equals the expected value of the denominator. This is an example of an exact F-test.

Notice, however, that for a very small Lake effect, there are no mean squares such that the expected value of the numerator equals the expected value of the denominator. Therefore, Minitab uses an approximate F-test. In this example, the mean square for Lake is divided by the mean square for the Supplement*Lake interaction. This results in an expected value of the numerator being approximately equal to that of the denominator if the Lake effect is very small.

About the "Denominator of F-test is zero or undefined" message

Minitab will display an error that the denominator of the F-test is zero or undefined for one of the following reasons:
  • There is not at least one degree of freedom for error.

  • The adjusted MS values are very small, and thus there is not enough precision to display the F and p-values. As a workaround, multiply the response column by 10. Then perform the same regression model, but instead use this new response column for the response.

    Note

    Multiplying the response values by 10 will not affect the F and p-values that Minitab displays the output. However, decimal position will be affected in the remaining output, specifically, the sequential sums of squares, Adj SS, Adj MS, Fit, standard error of the fits, and residual columns.

Fitted value

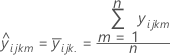
Notation

For a 3-factor model:

TermDescription
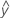the fitted value for the observation at the ith level of factor A, the jth level of factor B, the kth level of factor C
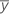the mean value for the observation at the ith level of factor A, the jth level of factor B, the kth level of factor C
nthe number of observations at the ith level of factor A, the jth level of factor B, the kth level of factor C

Residual (Resid)

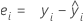
Notation

TermDescription
eii th residual
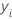i th observed response value
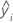i th fitted response
Copyright © 2024 Minitab, LLC. All rights Reserved.