In This Topic
Method
For two-factor models, analysis of means is a procedure to determine if the interaction effects are significant or the main effects are different from the grand mean. For two-way analysis of means, the data must be balanced.
Mean
Formula
The average of the observations for a factor at a given level. Minitab plots the mean for each factor level on the graph.
| Mean of Factor A at the ith level: |
 |
| Mean of Factor B at the jth level: |
 |
Notation
| Term | Description |
|---|---|
| yi. | sum of all observations for the ith level of factor A |
| y.j. | sum of all observations for the jth level of factor B |
| a | number of levels in A |
| b | number of levels in B |
| n | number of cases at the ith level of factor A and jth level of factor B |
Grand mean (center line)
Formula
The average of all observations in the sample. Minitab uses the grand mean as the center line on the graph of the main effects.

Notation
| Term | Description |
|---|---|
| y... | sum of all observations in the sample |
| a | number of levels in A |
| b | number of levels in B |
| n | number of cases at the ith level of factor A and jth level of factor B |
Upper and lower decision limits for main effects
The decision limits indicate whether factor level means are different from the grand mean. Points that lie outside the upper decision limit (UDL) or lower decision limit (LDL) are statistically different from the grand mean.
The calculation of the upper and lower decision limits varies based on the number of levels in the factor and the number of observations at each level. The formulas below show the upper and lower decision limits for factor A. To calculate the decision limits for factor B, replace terms specific to factor A with equivalent terms for factor B.
Two-level factor
The upper and lower decision limits for factor A are:
- UDLA =
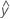 ...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...+ (.5) * hα* Sqrt[(MSE) * (2 / n1)] - LDLA =
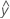 ...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
...- (.5) * hα* Sqrt[(MSE) * (2 / n1)]
where ha = absolute value(t(a / 2; abn - ab), MSE = mean square error (from an ANOVA with terms A, B, and AB) and n1 = number of observations at each level of the factor A.
Factor with more than two levels
- UDLA =
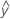 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
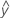 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
where MSE = mean square error (from an ANOVA with terms A, B, and AB), a = number of factor levels in factor A, and n1= number of observations at each level of the factor. The critical value hα depends on alpha, the number of means being plotted, and the degrees of freedom for MSE. You can find values for hα in Table B.1 in Appendix B in Nelson1.
For values of alpha outside the range of 0.001 and 0.1, the decision limits are:
- UDLA =
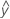 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
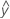 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
where MSE = mean square error (from an ANOVA with terms A, B, and AB), n1= number of observations at each level of the factor. and hα = absolute value (t(α2, df); where a2 = (1- (1- a )** (1 / a)) / 2 and df = nT - ab where nT = total number of observations in the sample,.
- L.S. Nelson (1983). "Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
Upper and lower decision limits for interaction effects
The decision limits indicate whether the interaction is significant. Points that lie outside the upper decision limit (UDL) or lower decision limit (LDL) indicate that the interaction is statistically significant.
Listed below are the general formulas for the upper and lower decision limits for the interaction of factors A and B. The terms are defined differently based on the number of levels and observations in each factor.
- UDLA B = hα* Sqrt[MSE * (q / (a * b * n)]
- LDLA B = –hα* Sqrt[MSE * (q / (a * b * n)]
where ha = absolute value (t(α2, dfe)), a = number of levels in factor A, b = number of levels in factor B, n = number of observations for each interaction between factors, q = degrees of freedom for interaction effects, (a - 1)(b - 1) and dfe = degrees of freedom for error, abn - ab.
Factors A and B both have two levels
- α2 = a / 2
Factor A has two levels and Factor B has more than two levels
- α2 = (1- (1- a )** (1 / b)) / 2
where a = number of levels in factor A and b = number of levels in factor B.
Factor A has more than two levels and Factor B two levels
- α2 = (1- (1- a )** (1 / a)) / 2
where a = number of levels in factor A and b = number of levels in factor B.
Factors A and B have more than two levels
- α2 = (1- (1- a )** (1 /a * b)) / 2
where a = number of levels in factor A and b = number of levels in factor B.
