In This Topic
Allocate the mean pool
Calculate adjusted means as follows:
μadj,i = μi + qiμPool
where
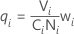
If you do not specify mean shift factors, then the mean pool = 0.
Allocate the variance pool
Calculate adjusted standard deviations as follows:
σ2adj,i = σ2i + riσ2Pool
where
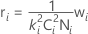
If you do not specify variation expansion factors and you do not specify both gap specification limits, then the variance pool = 0.
Notation
| Term | Description |
|---|---|
| Ci | Diametrical correction of the ith element |
| Di | Drift factor for the ith element |
| Ni | Complexity of the ith element |
| Si | Shift factor for the ith element |
| σi | Standard deviation of the ith element |
| σadj,i | Adjusted standard deviation of the ith element |
| T | Gap targeted value (if not available, T = μGap,ST) |
| Ti | Nominal value of the ith element |
| μi | Mean of the ith element |
| μadj,i | Adjusted mean of the ith element |
| Vi | Directional vector of the ith element |
| wi | Allocation weight for the mean pool or the variance pool, ith element |
| Z.BenchGap,LT | Benchmark Z (long-term) of the gap |
| Z.BenchGap,ST | Benchmark Z (short-term) of the gap |
| Z.Benchi,LT | Benchmark Z (long-term) of the ith element |
| Z.Benchi,ST | Benchmark Z (short-term) of the ith element |
| ZP | Z-value, which gives desired PPM (right tail) for long-term gap distribution |
