In This Topic
- Tolerance interval methods
- Exact nonparametric tolerance intervals for continuous distributions
- Lognormal distribution
- Approximate tolerance intervals for gamma distributions
- Exponential distribution
- Smallest extreme value distribution
- Weibull distribution
- Largest extreme value distribution
- Logistic distribution
- Loglogistic distribution
- Anderson-Darling test
Tolerance interval methods
- Lognormal
- Gamma
- Exponential
- Smallest extreme value
- Weibull
- Largest extreme value
- Logistic
- Loglogistic
General Definitions
Let X 1, X 2, ..., X n be the ordered statistics based on random sample of size n from some continuous distribution.
Let the distribution function be F(x;θ) for Ω in some parameter space with dimension greater than or equal to 1.
Let L < U be two statistics based on the sample such that for any given values α and P, with 0 < α < 1 and 0 < P < 1, the following holds for every θ in Ω:
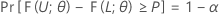
Then, the interval [L, U] is a two-sided tolerance interval with content = P x 100% and confidence level = 100(1 – α)%. Such an interval can be called a two-sided (1 – α, P) tolerance interval. For example, if α = 0.10 and P = 0.85, then the resulting interval is called a two-sided (90% , 0.85) tolerance interval.
If L = –∞ and U < +∞, then the interval (-∞, U] is called a one-sided (1 – α, P) upper tolerance bound. If L > -∞ and U = +∞, then the interval [L, +∞) is called a one-sided (1 – α, P) lower tolerance bound.
- A one-sided (1 – α, P) lower tolerance bound is also a one-sided (P, 1 – α) upper tolerance bound.
- A one-sided (1 – α )100% lower confidence bound of the (1 – P)th percentile of the distribution of the data is also a one-sided (1 – α, P) lower tolerance bound. Similarly, a one-sided (1 – α )100% upper confidence bound of the P th percentile of the distribution of the data is also a one-sided (1 – α , P) upper tolerance bound.
- If L and U are one-sided (1 – α/2 , (1 + P )/2) lower and upper tolerance bounds, then [ L, U ] is an approximate two-sided (1 – α, P ) tolerance interval. This method may be used in cases where two-sided tolerance intervals cannot be directly obtained. The resulting two-sided tolerance intervals are generally conservative. See Guenther1 and Hahn and Meeker2.
- Guenther, W. C. (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. and Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
Exact nonparametric tolerance intervals for continuous distributions
Minitab calculates exact (1 – α, P) nonparametric tolerance intervals, where 1 – α is the confidence level and P is the coverage (the target minimum percentage of population in the interval). The nonparametric method for tolerance intervals is a distribution free method. That is, the nonparametric tolerance interval does not depend on the parent population of your sample. Minitab uses an exact method for both one-sided and two-sided intervals.
Let X 1, X 2 , ... , X n be the ordered statistics based on a random sample from some continuously distributed population F(x;θ). Then, based on the findings of Wilks1, 2 and Robbins3, it can be shown that:

where B denotes the cumulative distribution function of the beta distribution with parameters a = r and b = n – s + 1. Thus ( Xr , Xs ) is a distribution-free tolerance interval because the coverage of the interval has a beta distribution with known parameter values, which are independent of the distribution of the parent population, F(x;θ).
One-sided intervals
Let k be the largest integer that satisfies the following:

where Y is a binomial random variable with parameters n and 1 – P. It can be shown (see Krishnamoorthy and Mathew4) that a one-sided (1 – α, P) lower tolerance bound is given by Xk . Similarly, a one-sided (1 – α, P) upper tolerance bound is given by X n - k +1. In both cases, the actual or effective coverage is given by P(Y > k).
Two-sided intervals
Let k be the smallest integer that satisfies the following:

where V is a binomial random variable with parameters n and P. Thus,
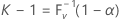
where F V -1(x) is the inverse cumulative distribution function of V. It can be shown (see Krishnamoorthy and Mathew4) that a two-sided (1 – α, P) tolerance interval may be given as ( Xr , Xs ). Minitab chooses s = n - r + 1 so that r = ( n – k + 1) / 2. Both r and s are rounded down to the nearest integer. The actual or effective coverage is given by P(V < k – 1).
Notation
| Term | Description |
|---|---|
| 1 – α | the confidence level of the tolerance interval |
| P | the coverage of the tolerance interval (the target minimum percentage of population in the interval) |
| n | the number of observations in the sample |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. and Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
Lognormal distribution
- Minitab takes the natural logarithm of the data.
- Minitab calculates a tolerance interval for the transformed data using the tolerance interval procedure for the normal distribution.
- Minitab exponentiates the limits of the tolerance interval obtained in the previous step to transform the interval to the scale of the original data.
Approximate tolerance intervals for gamma distributions
The tolerance interval for the gamma distribution uses an approximation to the normal distribution. Krishnamoorthy, et al. conduct simulation studies that show that the approximation provides accurate results. The calculations follow this process:
- Minitab takes the cubic root of the data.
- Minitab calculates a tolerance interval for the transformed data using the tolerance interval procedure for the normal distribution.
- Minitab exponentiates the limits of the tolerance interval obtained in the previous step to transform the interval to the scale of the original data.
- Krishnamoorthy K., Mathew T and Mukherjee S (2008). Normal based methods for a Gamma distribution: prediction and tolerance intervals and stress-strength reliability. Technometrics, 50, 69—78.
Exponential distribution
Minitab calculates exact (1 – α, P) tolerance intervals, where 1 – α is the confidence level and P is the coverage (the target minimum proportion of the population in the interval). The formulas differ between the calculation of one-sided tolerance limits and two-sided tolerance intervals.
One-sided exponential tolerance limits
This formula gives the lower limit:
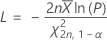
This formula gives the upper limit:

Two-sided exponential confidence intervals
Minitab uses Newton's method to solve the following system of equations. For more detail, see Fernandez1.
This formula gives the two-sided interval:

Where,

and the value of k 1 depends on the solution to this system of equations:

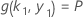
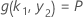
where,
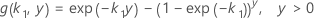
Notation
| Term | Description |
|---|---|
| n | the sample size |
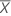 | the sample mean |
| P | the target minimum proportion of the population in the interval |
 | the α th percentile of the chi-square distribution with 2n degrees of freedom |
| α | 1 − confidence level |
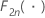 | the cumulative distribution function of the chi-square distribution with 2n degrees of freedom |
- Fernandez, Arturo J. (2010). Two-sided tolerance intervals in the exponential case: Corrigenda and generalizations. Computational Statistics and Data Analysis, 54, 151—162.
Smallest extreme value distribution
Minitab calculates exact (1 – α, P) tolerance intervals based on Lawless1, where 1 – α is the confidence level and P is the coverage (the target minimum percentage of population in the interval).
Exact one-sided smallest extreme value tolerance limits
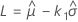
where


with
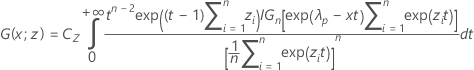
where

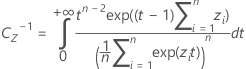
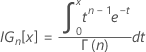
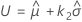
The value of k 2 comes from replacing α with 1 − α and P with 1 − P in the formulas for computing k 1.
Approximate two-sided smallest extreme value tolerance intervals
To calculate the approximate two-sided interval, replace α by α/2 and P by (P + 1)/2 in the formulas for computing the one-sided tolerance limits.
Notation
| Term | Description |
|---|---|
 | the maximum likelihood estimate of the location parameter of the extreme value distribution |
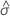 | the maximum likelihood estimate of the scale parameter of the extreme value distribution |
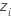 | 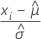 , the centered observations based on the MLE estimates of the location and scale parameters of the smallest extreme value distribution , the centered observations based on the MLE estimates of the location and scale parameters of the smallest extreme value distribution |
| t | the α th percentile of the non-central t-distribution with n − 1 degrees of freedom and noncentrality parameter δP |
| 1 - α | the confidence level of the tolerance interval |
| P | the coverage of the tolerance interval (the target minimum percentage of population in the interval) |
| n | the number of observations in the sample |
- Lawless, J. F. (1975). Construction of tolerance bounds for the extreme-value and the Weibull distribution. Technometrics, 17, 255—261.
Weibull distribution
- Minitab takes the natural logarithm of the data.
- Minitab calculates a tolerance interval for the transformed data using the tolerance interval procedure for the smallest extreme value distribution.
- Minitab exponentiates the limits of the tolerance interval obtained in the previous step to transform the interval to the scale of the original data.
Largest extreme value distribution
- Minitab multiplies the data by −1.
- Minitab calculates a tolerance for the transformed data using the tolerance interval procedure for the smallest extreme value distribution.
- Minitab exponentiates the limits of the tolerance interval obtained in the previous step to transform the interval to the scale of the original data.
For formulas that apply to the smallest extreme value distribution, go to the section on the smallest extreme value distribution.
Logistic distribution
Minitab calculates approximate (1 − α, P) tolerance intervals based on Bain and Engelhardt1, where 1 − α is the confidence level and P is the coverage (the target minimum percentage of population in the interval). The formula for the lower tolerance factor differs from the formula for the upper tolerance factor.
One-sided logistic tolerance limits
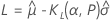
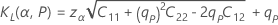
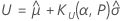
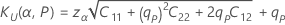
Two-sided logistic tolerance intervals
The analysis produces an approximate two-sided tolerance interval for the logistic distribution with Bonferroni's inequality2. This approximation method replaces α by α/2 and P by (P + 1)/2 in the formulas for computing the one-sided tolerance limits.
Notation
| Term | Description |
|---|---|
 | the lower tolerance factor |
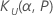 | the upper tolerance factor |
| zα | the upper α percentile of the standard normal distribution, which is equivalent to the lower 1 −α percentile point |
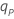 | log(p) − log(1 − p), the p × 100 lower percentile of the standard logistic distribution |
| C11 | 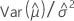 |
| C22 |  |
| C12 | 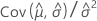 |
 | the maximum likelihood estimate of the logistic location parameter |
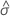 | the maximum likelihood estimate of the logistic scale parameter |
- Bain, L. and Englehardt, M. (1991). Statistical analysis of reliability and life testing models: Theory and methods. Second edition, Marcel Dekker, Inc.
- Hahn, G. J. and Meeker, W. Q. (2017). Statistical intervals: A guide for practitioners. Second edition, John Wiley and Sons, Inc.
Loglogistic distribution
- Minitab takes the natural logarithm of the data.
- Minitab calculates a tolerance interval for the transformed data using the tolerance interval procedure for the logistic distribution.
- Minitab exponentiates the limits of the tolerance interval obtained in the previous step to transform the interval to the scale of the original data.
For formulas that apply to the logistic distribution, go to the section on the logistic distribution.
Anderson-Darling test
Minitab uses Anderson-Darling statistics to perform the goodness-of-fit test.
Let Z = F(X), where F(X) is the cumulative distribution function. Suppose that a sample X1, .., Xn gives values Z(i) = F(Xi), i=1,.., n. Rearrange Z(i) in ascending order, Z(1) < Z(2) <...<Z(n). Then the Anderson-Darling statistic (A2) is calculated as follows:
- A2 = –n - (1/n) Σi[(2i – 1) log Z(i) + (2n + 1 – 2i) log (1 – Z(i))]
The modified Anderson-Darling goodness-of-fit test statistic is calculated for each distribution. The p-values are based on the table given by D'Agostino and Stephens.1 If no exact p-value is found in the table, Minitab calculates the p-value based on interpolation using the range of the p-value.
