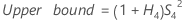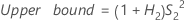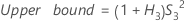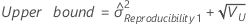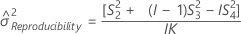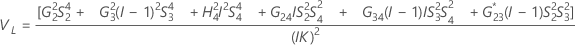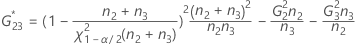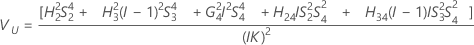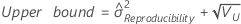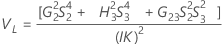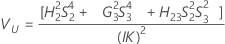In This Topic
- Common notation and rules for Gage R&R confidence intervals
- Repeatability variance component confidence interval
- Reproducibility (or Operator) variance component confidence interval
- Operator variance component confidence interval
- Interaction variance component confidence interval
- Total gage variance component confidence interval
- Part-to-part variance component confidence interval
- Total variance component confidence interval
Common notation and rules for Gage R&R confidence intervals
For all variance components, lower and upper bounds for variance components must not be negative values. If the bounds calculated using the formulas are negative, then they are set to zero.
For all ratios between 0 and 1, lower and upper bounds should also be between 0 and 1. If the bounds are outside the range, they are set to 0 or 1 accordingly.
Notation
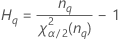
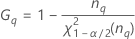
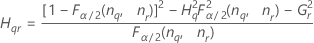
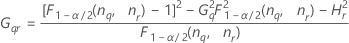
| Term | Description |
|---|---|
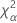 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| Fα(nq, nγ) | the α *100 percentile of the F distribution with nq and nγ degrees of freedom |
| I | the number of parts |
| J | the number of operators |
| K | the number of replicates |
For degrees of freedom:
Parts: n1=I–1
Operators: n2=J–1
Parts*Operators: n3=(I–1)(J–1)
Replicates: n4=IJ(K–1)
MSPart = S12
MSOperator = S22
MSPart*Operator = S32
MSReplicates = S42
Repeatability variance component confidence interval
Minitab calculates the lower and upper bounds for an exact (1 – α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
Formulas
- With operator
-
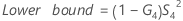
- Without operator
-

- Without interaction term
-

Notation
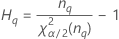
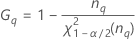
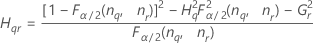
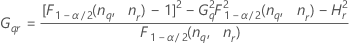
| Term | Description |
|---|---|
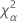 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Reproducibility (or Operator) variance component confidence interval
Minitab uses the modified large-sample (MLS) method to calculate the lower and upper bounds for an approximate (1 – α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
Formulas
- With interaction term
-
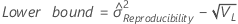
- Without interaction term
-
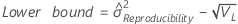
Notation
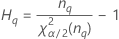
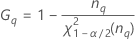
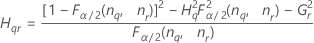
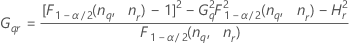
| Term | Description |
|---|---|
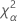 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Operator variance component confidence interval
Minitab uses the modified large-sample (MLS) method to calculate the lower and upper bounds for an approximate (1–α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
Formulas


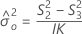
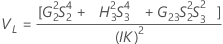
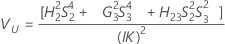
Notation
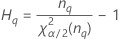
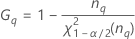
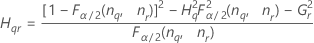
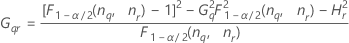
| Term | Description |
|---|---|
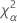 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Interaction variance component confidence interval
Minitab uses the modified large-sample (MLS) method to calculate the lower and upper bounds for an approximate (1 – α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
Formulas


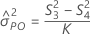

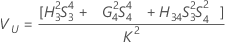
Notation
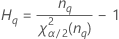

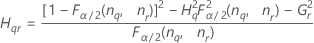
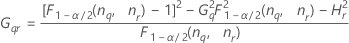
| Term | Description |
|---|---|
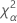 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Total gage variance component confidence interval
With operator and interaction term
Minitab uses the modified large-sample (MLS) method to calculate the lower and upper bounds for an approximate (1 – α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.



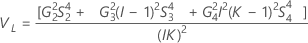
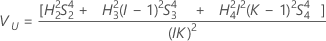
Without operator term
The lower and upper bounds for an exact (1 – α) *100% confidence interval are:


Without interaction term
Minitab uses the modified large-sample (MLS) method, the lower and upper bounds for an approximate (1 – α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.


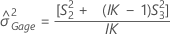
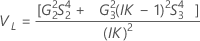
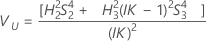
Notation
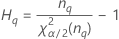
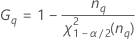
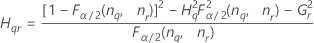
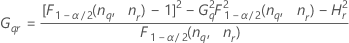
| Term | Description |
|---|---|
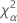 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Part-to-part variance component confidence interval
Minitab uses the modified large-sample (MLS) method to calculate the lower and upper bounds for an approximate (1 – α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
With operator



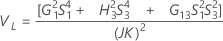
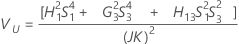
Without operator


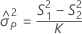
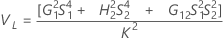
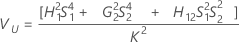
Without interaction



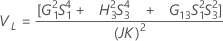
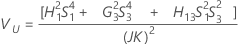
Notation
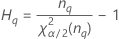
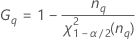
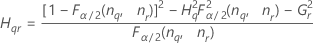
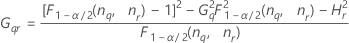
| Term | Description |
|---|---|
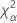 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Total variance component confidence interval
Minitab uses the modified large-sample (MLS) method to calculate the lower and upper bounds for an approximate (1 – α) *100% confidence interval. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
With operator



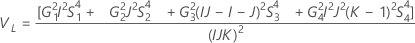
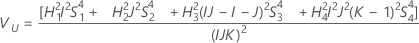
Without operator


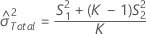
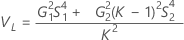

Without interaction term


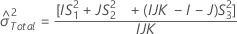

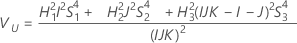
Notation
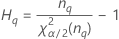
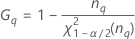
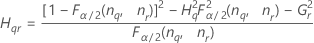

| Term | Description |
|---|---|
 | the α *100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |