In This Topic
Display additional σ limits at
In These multiples of the standard deviation, enter one or more values to display additional standard deviation lines on your control chart.
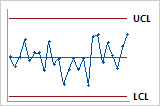
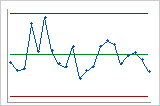
Default 3 sigma limits
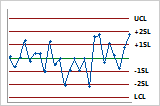
Additional sigma limits at 1 and 2 standard deviations
Place bounds on control limits
You can specify a lower bound and an upper bound for the control limits. If the calculated control limit is farther from the center line than the value that you specify, Minitab displays the bound instead of the control limit. Minitab labels the lower bound as LB and the upper bound as UB.
Note
Upper bounds and lower bounds do not affect the calculations for any of the tests for special causes.
Force control limits to be straight
By default, Minitab calculates the control limits using the actual subgroup sizes. When the subgroup sizes differ, the control limits are uneven, but you can force the control limits to be straight. Under When subgroup sizes are unequal, calculate control limits, select Assuming all subgroups have size, and enter a subgroup size.
This option is especially useful when all subgroups were intended to be the same size, but some subgroups are a different size. For example, some subgroups are smaller because of missed measurements. In that case, set the subgroup size to the intended size.
You will not get truly constant limits when you assume constant subgroups with Moving Average chart. If you have a moving average of length K, the control limits for the first K – 1 moving averages will be different because of the different number of data values used in each of those first K −1 moving average values. After the kth moving average, you will get constant limits.
CAUTION
When you specify a subgroup size, you change the calculations for the control limits, which can change the results of the tests for special causes. Use this option only if the differences between the subgroup sizes are small. Don't use this option when the difference between subgroup sizes is more than 25%. For example, if the largest subgroup has 10 observations and the smallest subgroup has 8 observations, then the difference is 20% ((10 – 8) / 10 = 0.2 = 20%).
For example, the data for the following charts is the same, but the control limits for the second chart were calculated based on a fixed subgroup size.
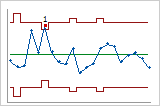
Actual subgroup sizes