In This Topic
Step 1: Determine whether the process variability is in control
The generalized variance chart plots the joint process variability of several related variables. The center line is the determinant of the sample covariance matrix. The lower and upper control limits are based on the number of variables and number of observations in each subgroup.
The Generalized Variance chart should be in control before you interpret the Tsquared chart. When the Generalized Variance chart is out of control, the control limits on the Tsquared chart will not be accurate and may falsely indicate an out-of-control condition.
Red points indicate subgroups that are above the upper control limit and not in control. One disadvantage to multivariate charts is that the scale is unrelated to the scale of any of the variables, and out-of-control signals do not reveal which variable (or combination of variables) caused the signal.
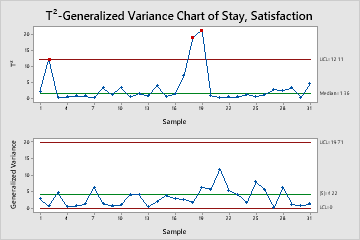
In these results, the generalized variance chart (the bottom chart) shows no out-of-control points.
Step 2: Determine whether the process location is in control
The T2 chart plots the T2 for each subgroup to measure whether the process locations of several related variables are simultaneously in control. The center line is the median of the theoretical distribution of T2 statistics. The upper control limit is based on the number of samples, the size of each sample, and the number of variables.
Minitab identifies points that are outside the control limit with a red symbol. Out-of-control points may indicate the presence of special causes. One disadvantage to multivariate charts is that the scale is unrelated to the scale of any of the variables, and out-of-control signals do not reveal which variable (or combination of variables) caused the signal.

In these results, look at the Tsquared chart. Three points are out of control. Subgroups 2, 18, and 19 are above the upper control limit, which indicates that special causes may currently affect the process. When you hold the pointer over a red point, you can get more information about this subgroup.
Step 3: Identify which points failed the test
Investigate any points that are above the upper control limit. The output shows exactly which points are above the control limit, as shown here.
