Complete the following steps to create a plot that shows x-values and probabilities in a shaded area.
- Choose .
- Select the distribution and enter the parameters for the distribution. For more information, go to Select the distribution and parameters.
- Click the Shaded Area tab. In Define Shaded Area By, select either Probability or X value. Minitab calculates the value that is not specified.
- Select the area of the plot that you want to shade.
- Right Tail: Shade the area of values that are greater than the probability or x-value that you enter.
- Left Tail: Shade the area of values that are less than the probability or x-value that you enter.
- Both Tails: Shade the area of values that have equal probabilities.
- Middle: Shade the area of the values that you entered.
- Enter one or more probabilities or x-values that define the endpoints.
Examples of shaded areas
The following graphs model scores for an entrance exam into an education program. The scores are normally distributed with a known mean and standard deviation.
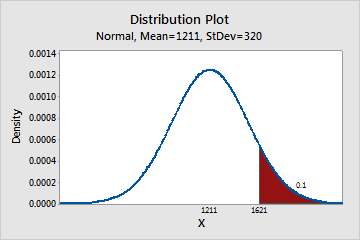
- Right tail
-
Students must score in the top 10 percent to be accepted into the program. The following graph shows that students who have scores of 1621 or greater are in the top 10 percent.
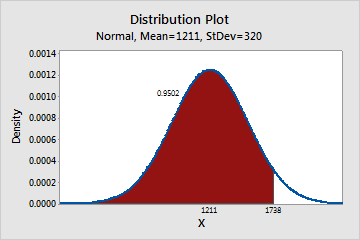
- Left tail
-
You received a score of 1738 and want to know your percentile. Your score of 1738 is at the 95th percentile.
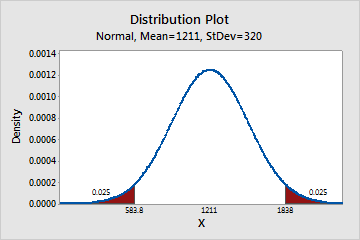
- Both tails
-
You want to know the scores at the 2.5th percentile and the 97.5th percentile. At the 2.5th percentile, the score is 583.8 and at the 97.5th percentile, the score is 1838. Approximately 95% of the students have scores that are between 583 and 1838.
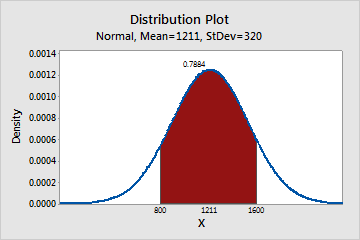
- Middle
-
You want to know what percentage of students has scores that are between 800 and 1600. Approximately 79% of the students have scores that are between 800 and 1600.