Select the method or formula of your choice.
Test mean – target (Difference)
Power
Let tα,v be the upper α (one-sided) critical value for a t-distribution with v degrees of freedom. The power for the two-sided alternative hypothesis Lower limit < test mean - target < upper limit is given by:
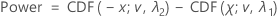
For alternative hypotheses of Test mean > target or Test mean - target > lower limit, the power is given by:

For alternative hypotheses of Test mean < target or Test mean - target < upper limit, the power is given by:

where CDF( x ; v , λ ) is the cumulative distribution function, evaluated at x, for a noncentral t-distribution with noncentrality parameter, λ , and v degrees of freedom.
Degrees of freedom
The degrees of freedom, v, is given by:

Noncentrality parameters
The noncentrality parameter that corresponds to the lower equivalence limit is denoted as λ1, and is given by:
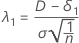
For the alternative hypothesis Test mean > target, δ1 = 0.
The noncentrality parameter that corresponds to the upper equivalence limit is denoted as λ2, and is given by:
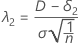
For the alternative hypothesis Test mean < target, δ2 = 0.
Notation
| Term | Description |
|---|---|
| α | significance level for the test |
| D | mean of the test population minus the target value |
| δ1 | lower equivalence limit |
| δ2 | upper equivalence limit |
| n | sample size |
| σ | standard deviation of the population |
