In This Topic
S
The test statistic has an approximately chi-square ( χ2) distribution, with associated degrees of freedom (k – 1). If the data within one or more blocks have ties, Minitab uses the average rank and prints a test statistic that has been corrected for ties. For details about this method, see M. Hollander and D.A. Wolfe (1973)1.
Formula
To calculate the chi-square test statistic, Minitab ranks the data separately within each block and sums the ranks for each treatment.
If the data have no ties, the formula is:
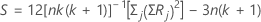
If the data have ties, the formula is:

where C is a correction factor that is equal to:
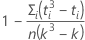
Notation
| Term | Description |
|---|---|
| j | 1, 2, ..., k |
| k | the number of treatment conditions |
| n | the number of blocks |
| Rj | the sum of ranks for treatment j |
| i | 1, 2, ..., m |
| m | the number of sets of ties |
| ti | the number of tied scores in the ithset of ties |
- M. Hollander and D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc.
Grand median
To understand how to calculate the treatment effects, the block medians, and the grand median, consider the following data.
| Block | ||||
| Treatment | 1 | 2 | 3 | 4 |
| 1 | 0.15 | 0.26 | 0.23 | 0.99 |
| 2 | 0.55 | 0.26 | −0.22 | 0.99 |
| 3 | 0.55 | 0.66 | 0.77 | 0.99 |
To calculate treatment effects (Doksum method1), first find the median difference between pairs of treatments. The pairwise differences for treatment 1 minus treatment 2 are 0.15 - 0.55 = −0.4, 0.26 – 0.26 = 0, 0.23 – (−0.22) = 0.45, and 0.99 – 0.99 = 0. The median of the differences is 0. Performing this calculation for the other two pairs gives −0.4 for treatment 1 minus treatment 3, and −0.2 for treatment 2 minus treatment 3.
The effect for each treatment is the average of the median differences of that treatment with all other treatments (including itself). For the data in this example, effect(2) = [median (2 – 1) + median (2 – 2) + median (2 – 3)]/3 = (0.00 + 0.00 – 0.20)/3 = −0.0667. Similarly, effect(1) = −0.1333 and effect(3) = 0.20.
To calculate adjusted block medians, adjust each observation by subtracting the appropriate treatment effect from the observation. Adjusted block medians are simply the medians of these adjusted data, calculated within each block. The grand median is the median of the adjusted block medians. The estimated median for each treatment level is the treatment effect plus the grand median.
- M. Hollander and D.A. Wolfe (1973). Nonparametric Statistical Methods, John Wiley & Sons, Inc., pp. 158 – 161.
Ranking tied values
- Sort the observations in ascending order.
- Assign ranks to each observation as if there were no ties.
- For a tied set, take the average of the corresponding ranks and assign this value as the new rank to each tied value in that set.
Example
A sample has 9 observations: 2.4, 5.3, 2.4, 4.0, 1.2, 3.6, 4.0, 4.3, and 4.0
| Observation | Rank (assuming no ties) | Rank |
|---|---|---|
| 1.2 | 1 | 1 |
| 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 |
| 3.6 | 4 | 4 |
| 4.0 | 5 | 6 |
| 4.0 | 6 | 6 |
| 4.0 | 7 | 6 |
| 4.3 | 8 | 8 |
| 5.3 | 9 | 9 |
- The number of sets of ties = 2
- The number of tied values in the first set = 2
- The number of tied values in the second set = 3
