In This Topic
Step 1: Determine whether the test mean and the reference mean are equivalent
Compare the confidence interval with the equivalence limits. If the confidence interval is completely within the equivalence limits, you can claim that the mean of the test population is equivalent to the mean of the reference population. If part of the confidence interval is outside the equivalence limits, you cannot claim equivalence.
Difference: Mean(Discount) - Mean(Original)
| Difference | SE | 95% CI for Equivalence | Equivalence Interval |
|---|---|---|---|
| -0.12122 | 0.20324 | (-0.483449, 0.241005) | (-0.5, 0.5) |
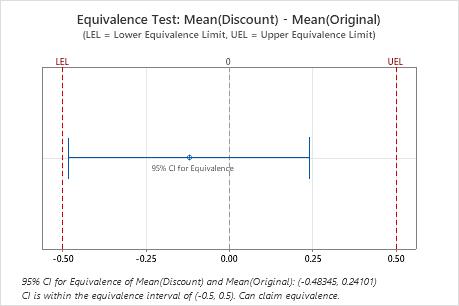
Key Results: 95% CI, Equivalence interval
In these results, the 95% confidence interval is completely within the equivalence interval defined by the lower equivalence limit (LEL) and the upper equivalence limit (UEL). Therefore, you can conclude that the test mean is equivalent to the reference mean.
Note
You can also use the p-values to evaluate the results of the equivalence test. To demonstrate equivalence, the p-values for both null hypotheses must be less than alpha.
Step 2: Check your data for problems
Problems with your data, such as skewness or outliers, can adversely affect your results. Use graphs to look for skewness (by examining the spread of the data) and to identify potential outliers.
Determine whether the data appear to be skewed
When data are skewed, the majority of the data is toward the high or low side of the graph. Often, skewness is easiest to identify with a boxplot or histogram.
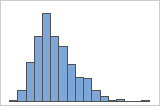
Right-skewed
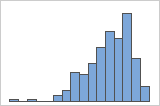
Left-skewed
For example, the right-skewed histogram shows salary data. Many employees are paid a relatively small amount, while increasingly few employees are paid large salaries. The left-skewed histogram shows failure rate data. A few items fail earlier while an increasing number of items fail later.
Data that are severely skewed can affect the validity of the test results if your sample is small (< 20 values). If your data are severely skewed and you have a small sample, consider increasing your sample size.
Identify outliers
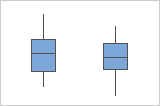
Outliers, which are data points that are far away from most of the other data, can strongly affect your results. Outliers are easiest to identify on a boxplot.
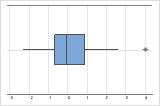
On a boxplot, outliers are identified by asterisks (*).
You should try to identify the cause of any outliers. Correct any data entry or measurement errors. Consider removing data that are associated with special causes and repeating the analysis. For more information on special causes, go to Using control charts to detect common-cause variation and special-cause variation.
Compare the spread of the data (optional)
Note
To formally check for equal variances, use the test for 2 Variances.
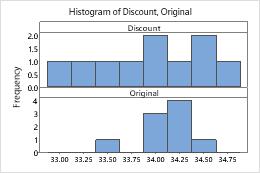
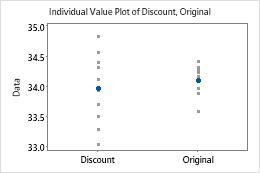
In these graphs, the data do not appear to be skewed and there are no outliers.
The spread of the data does not appear to be the same for the test group and the reference group. Therefore, you should not assume equal variances for the test.
