The degrees of freedom (DF) are the amount of information your data provide that you can "spend" to estimate the values of unknown population parameters, and calculate the variability of these estimates. This value is determined by the number of observations in your sample and the number of parameters in your model.
Increasing your sample size provides more information about the population, and thus increases the degrees of freedom in your data. Adding parameters to your model (by increasing the number of terms in a regression equation, for example) "spends" information from your data, and lowers the degrees of freedom available to estimate the variability of the parameter estimates.
Degrees of freedom are also used to characterize a specific distribution. Many families of distributions, like t, F, and chi-square, use degrees of freedom to specify which specific t, F, or chi-square distribution is appropriate for different sample sizes and different numbers of model parameters. For example, the following figure depicts the differences between chi-square distributions with different degrees of freedom.
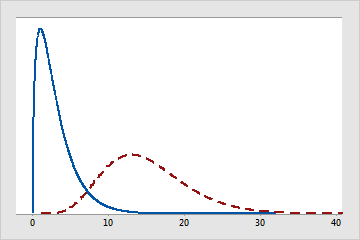
Chi-square distributions with different degrees of freedom
The solid-line distribution has 3 degrees of freedom. The dashed-line distribution has 15 degrees of freedom.
Examples
For example, the 1-sample t-test estimates only one parameter: the population mean. The sample size of n constitutes n pieces of information for estimating the population mean and its variability. One degree of freedom is spent estimating the mean, and the remaining n-1 degrees of freedom estimate variability. Therefore, a 1-sample t-test uses a t-distribution with n-1 degrees of freedom.
Conversely, multiple linear regression must estimate a parameter for every term you choose to include in the model, and each one consumes a degree of freedom. Therefore, including excessive terms in a multiple linear regression model reduces the degrees of freedom available to estimate the parameters' variability, and can make it less reliable.
