Sum of squares (SS)
In matrix terms, these are the formulas for the different sums of squares:

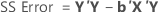

Minitab breaks down the SS Regression or SS Treatments component into the amount of variation explained by each term using both the sequential sum of squares and adjusted sum of squares.
Notation
| Term | Description |
|---|---|
| b | vector of coefficients |
| X | design matrix |
| Y | vector of response values |
| n | number of observations |
| J | n by n matrix of 1s |
Adj MS – Regression
The formula for the Mean Square (MS) of the regression is:
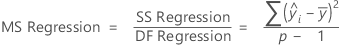
Notation
| Term | Description |
|---|---|
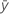 | mean response |
 | ith fitted response |
| p | number of terms in the model |
Adj MS – Error
The Mean Square of the error (also abbreviated as MS Error or MSE, and denoted as s2) is the variance around the fitted regression line. The formula is:

Notation
| Term | Description |
|---|---|
| yi | ith observed response value |
 | ith fitted response |
| n | number of observations |
| p | number of coefficients in the model, not counting the constant |
F
If all the factors in the model are fixed, then the calculation of the F-statistic depends on what the hypothesis test is about, as follows:
- F(Term)
-

- F(Lack-of-fit)
-

If there are random factors in the model, F is constructed using the expected mean square information for each term. For more information, see Neter et al.1.
Notation
| Term | Description |
|---|---|
| Adj MS Term | A measure of the amount of variation that a term explains after accounting for the other terms in the model. |
| MS Error | A measure of the variation that the model does not explain. |
| MS Lack-of-fit | A measure of variation in the response that could be modeled by adding more terms to the model. |
| MS Pure error | A measure of the variation in replicated response data. |
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.
p-value (P)
Used in hypothesis tests to help you decide whether to reject or fail to reject a null hypothesis. The p-value is the probability of obtaining a test statistic that is at least as extreme as the actual calculated value, if the null hypothesis is true. A commonly used cut-off value for the p-value is 0.05. For example, if the calculated p-value of a test statistic is less than 0.05, you reject the null hypothesis.
