In This Topic
Coefficients and standardized coefficients
Coefficients are the parameters in a regression equation. The estimated coefficients are used with the predictors to calculate the fitted value of the response variable and the predicted response of new observations. In contrast to least squares, the PLS coefficients are nonlinear estimators. Standardized coefficients indicate the importance of each predictor in the model and correspond to the standardized x- and y-variables. In PLS, the coefficient matrix (dimension p × r) is calculated from the weights and loadings.
The formula for standardized coefficients is:

To calculate the nonstandardized coefficients and intercept, use these formulas:
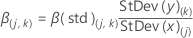

Notation
| Term | Description |
|---|---|
| W | the x-weight matrix |
| P | the x-loading matrix |
| C | the y-loading matrix |
| j | the predictors (1, p) |
| k | the responses (1, r) |
| p | the number of predictors |
| r | the number of responses |
Leverages
In least squares regression, leverages are values that indicate how far the corresponding observations are from the center of the x-space, which is described by the x-values. In PLS, the predictors are replaced by x-scores. Observations with high leverage have x-scores far from zero and have a significant influence on the regression coefficients. Points with high leverage are outliers in the x-space, but are not necessarily outliers in the y-space.
The leverage values in PLS are calculated from the x-score matrix T, which is used to calculate the hat matrix (H) as follows:

The leverage (hii) of the ith observation is the ith diagonal element of the H matrix.
A leverage value greater than 2m / n is considered high and should be examined.
Notation
| Term | Description |
|---|---|
| n | the number of observations |
| m | the number of components |
Distances from the x-model
A measure of how well observations are fitted in the x-space; indicates how well the x-scores describe observations. An observation with a large distance may also be a leverage point.
Formula
The formula for calculating the distance from the x-model for the ith observation is:
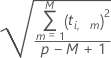
Notation
| Term | Description |
|---|---|
| M | number of components |
| t | x-score |
| p | number of predictors |
Distances from the y-model
A measure of how well observations are fitted in the y-space; indicates how well the y-scores describe observations. An observation with a large distance may also be an outlier.
Formula
The formula for calculating the distance from the y-model for the ith observation follows:
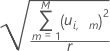
Notation
| Term | Description |
|---|---|
| M | the number of components |
| u | the y-score |
| r | the number of responses |
