In This Topic
Leverages (Hi)
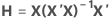
The leverage of the ith observation is the ith diagonal element, hi of H. If hi is large, the ith observation has unusual predictors (X1i, X2i, ..., Xpi). That is, the predictor values are far from the mean vector (X1, X2,..., Xp), using Mahalanobis distance.
Leverage values fall between 0 and 1. Minitab identifies observations with leverages over 3p/n or .99, whichever is smaller, with an X in the table of unusual observations. Usually, you examine values with large leverages.
Notation
| Term | Description |
|---|---|
| X | design matrix |
| hi | ith diagonal element of the hat matrix |
| p | number of terms in the model |
| n | number of observations |
Cook's distance
Overall measure, D, of the combined impact across all of the estimated regression coefficients on an observation. Minitab calculates D using leverage values and standardized residuals, and considers whether an observation is unusual with respect to both x- and y-values. Observations with large D values may be outliers.
Formula
Cook's distance is the distance between the coefficients calculated with and without the i th observation. Minitab calculates Cook's distance without fitting a new regression equation each time an observation is omitted. This calculation is:

Notation
| Term | Description |
|---|---|
| ei | i th residual |
| hi | i th diagonal element of 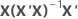 |
| p | number of model parameters |
| s 2 | mean square error |
| b | coefficient vector |
| b(i) | coefficient vector calculated after deleting the i th observation |
| X | design matrix |
DFITS
Combines leverage and studentized residual (deleted t residuals) values into one overall measure of how unusual an observation is. DFITS measures the influence of each observation on the fitted values in a regression and ANOVA model. Observations with large DFITS values may be outliers.
DFITS represents roughly the number of standard deviations that the fitted value changes when each observation is removed from the data set and the model is refit. Minitab can calculate DFITS without fitting a new regression equation each time an observation is omitted.
Formula

Notation
| Term | Description |
|---|---|
| ei | i th residual |
| hi | i th diagonal element of 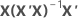 |
| X | design matrix |
 | i th fitted response |
 | fitted value calculated without the i th observation |
| MSE (i) | mean square error calculated without the i th observation |
| n | number of observations |
| p | number of model parameters |
