The process standard deviation is also called sigma, or σ. If you enter an historical value for sigma, then Minitab uses the historical value. Otherwise, Minitab uses one of the following methods to estimate sigma from the data.
Sbar method
Without unbiasing constant
If you do not use an unbiasing constant, then the Sbar is the mean of the subgroup standard deviations:
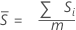
With unbiasing constant
If you use the unbiasing constant, c4(ni), then Sbar is calculated as follows:
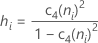
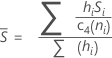
When the subgroup size is constant, Sbar is:
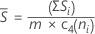
Notation
| Term | Description |
|---|---|
| c4 (ni) | value of the unbiasing constant c4 that corresponds to the value that is specified in parentheses. |
| Si | standard deviation of subgroup i |
| m | number of subgroups |
Pooled standard deviation method
The pooled standard deviation (Sp) is given by the following formula:
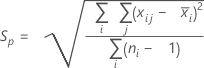
When the subgroup size is constant, Sp can also be calculated as follows:

With unbiasing constant
By default, Minitab applies the unbiasing constant, c4(), when you use the pooled standard deviation to estimate σ:
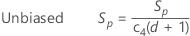
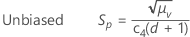
Notation
| Term | Description |
|---|---|
| xij | jth observation in the ith subgroup |
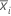 | mean of subgroup i |
| ni | number of observations in subgroup i |
| μv | mean of the subgroup variances |
| c4(·) | value of the unbiasing constant c4 that corresponds to the value that is specified in parentheses. |
| d | degrees of freedom for Sp, given by the following formula:
 |
Unbiasing constants c4() and c5()
c4()

c5()

Notation
| Term | Description |
|---|---|
| Γ() | gamma function |
