In This Topic
Pp

Notation
| Term | Description |
|---|---|
| USL | Upper specification limit |
| LSL | Lower specification limit |
| Toler | Multiplier of the sigma tolerance (Minitab uses 6 as the default value) |
 | Overall standard deviation |
Pp confidence interval bounds
The (1 -α) 100% confidence interval for Pp is calculated as follows:


Notation
| Term | Description |
|---|---|
| χ2α,ν | The α percentile of the chi-square distribution with ν degrees of freedom |
| α | Alpha for the confidence level |
| ν | The degrees of freedom (Σni– 1) |
| ni |
The number of observations in the ith subgroup |
PPL

Notation
| Term | Description |
|---|---|
 | Process mean (estimated from the sample data or a historical value) |
| LSL | Lower specification limit |
| Toler | Multiplier of the sigma tolerance (Minitab uses 6 as the default value) |
 | Overall standard deviation |
PPU

Notation
| Term | Description |
|---|---|
| USL | Upper specification limit |
 | Process mean (estimated from the sample data or a historical value) |
| Toler | Multiplier of the sigma tolerance (Minitab uses 6 as the default value) |
 | Overall standard deviation |
Ppk

Ppk confidence interval bounds
The (1 -α) 100% confidence interval for Ppk is calculated as follows:
Notation
| Term | Description |
|---|---|
| N | The total number of observations |
| α | Alpha for the confidence level |
| v | The degrees of freedom (Σni – 1 or N – 1) |
| ni | The number of observations in the ith subgroup |
| Toler | Multiplier of the sigma tolerance (Minitab uses 6 as the default value) |
| Z1–α/2 | The 1 – (α/2) percentile from the standard normal distribution |
Cpm
Cpm is available only when a target is specified. Minitab calculates Cpm based on known values of LSL, USL, and T.
| Known value | Cpm |
|---|---|
| LSL and USL only | * |
| LSL, USL, and T = m |
 |
| LSL, USL, and T ≠ m |
 |
| USL and T only |
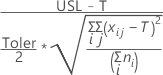 |
| LSL and T only |
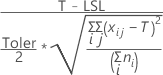 |
| Either LSL or USL only | * |
Notation
| Term | Description |
|---|---|
| * | Missing value |
| USL | Upper specification limit |
| LSL | Lower specification limit |
| m | Midpoint between USL and LSL |
| T | Target value |
| Xij | jth observation in the ith subgroup |
| ni | Number of observations in the ith subgroup |
| Toler | Multiplier of the sigma tolerance (Minitab uses 6 as the default value) |
Cpm confidence interval and bound
Minitab calculates the (1 – α) 100% two-sided confidence interval for Cpm as follows:
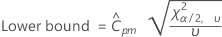

The (1 – α) 100% lower confidence bound for Cpm is calculated as follows:
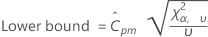
Notation
| Term | Description |
|---|---|
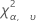 | α quantile of the chi-square distribution with ν degrees of freedom |
 | Degrees of freedom, defined as N ((1 + a2) 2 / (1 + 2a2)) |
| a | (Mean – Target)/ |
| α | Alpha for the confidence level |
| N | Total number of observations |
