In This Topic
- PPM < LSL for expected "within" performance
- PPM > USL for expected "within" performance
- PPM Total for expected "within" performance
- Confidence intervals for PPM total for expected "within" performance when both LSL and USL are known
- Confidence intervals for PPM total for expected “within” performance for a process with one specification limit
PPM < LSL for expected "within" performance

PPM < LSL and % < LSL are multiples of the probability:

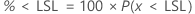
Two-sided confidence intervals
Confidence intervals for P(x < LSL) are given by the following formulas:


where
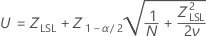
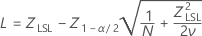

Confidence intervals for PPM < LSL and % < LSL are found by multiplying the confidence intervals for the probability by a constant.
PPM


%
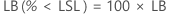
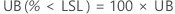
One-sided confidence bound
For a one-sided bound, the calculations follow:

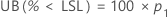
Minitab solves the following equation to find p1:
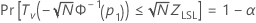
where

Notation
Notation
| Term | Description |
|---|---|
| LSL | the lower specification limit |
| USL | the upper specification limit |
| LB | the lower bound |
| UB | the upper bound |
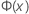 | the Cumulative Distribution Function (CDF) from a standard normal distribution |
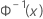 | the inverse CDF from a standard normal distribution |
 | the (1 - α/2)th percentile of the standard normal distribution |
| α | the alpha for the confidence level |
 | the process mean (estimated from the sample date or a historical value) |
| s | the sample standard deviation within subgroups |
| N | the total number of measurements |
| υ | the degrees of freedom for s |
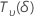 | a random variable that is distributed as a non-central t distribution with  degrees of freedom and non-centrality parameter δ degrees of freedom and non-centrality parameter δ |
PPM > USL for expected "within" performance
The parts per million greater than the upper specification limit (PPM > USL) and the percentage greater than the upper specification limit (% > USL) are both found from the probability that a part is above the specification limit (P(x > USL)).

PPM > USL and % > USL are multiples of the probability:
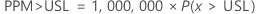
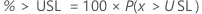
Two-sided confidence intervals
Confidence intervals for P(x > USL) are given by the following formulas:


where
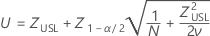
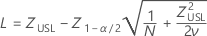

Confidence intervals for PPM > USL and % > USL are found by multiplying the confidence intervals for the probability by a constant.
PPM


%
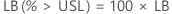

One-sided confidence bound
For a one-sided bound, the calculations follow:

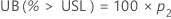
Minitab solves the following equation to find p1:
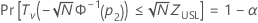
where

Notation
| Term | Description |
|---|---|
| USL | the upper specification limit |
| PPM | the parts per million |
| LB | the lower bound |
| UB | the upper bound |
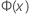 | the Cumulative Distribution Function (CDF) from a standard normal distribution |
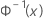 | the inverse CDF from a standard normal distribution |
 | the (1 - α/2)th percentile of the standard normal distribution |
| α | the alpha for the confidence level |
 | the process mean (estimated from the sample date or a historical value) |
| s | the sample standard deviation within subgroups |
| N | the total number of measurements |
| υ | the degrees of freedom for s |
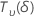 | a random variable that is distributed as a non-central t distribution with  degrees of freedom and non-centrality parameter δ degrees of freedom and non-centrality parameter δ |
PPM Total for expected "within" performance
The expected number of parts per million that are outside the specification limits, based on the variation within the subgroups, is

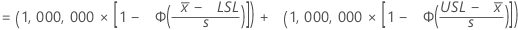
Notation
| Term | Description |
|---|---|
| PPM | Parts per million |
| LSL | Lower specification limit |
| USL | Upper specification limit |
| Φ (X) | Cumulative distribution function (CDF) of a standard normal distribution |
 | Average of the observations |
| s | Within-subgroup standard deviation |
Confidence intervals for PPM total for expected "within" performance when both LSL and USL are known
The total Parts Per Million (PPM) out-of-specification and the percentage out-of-specification are both found from the probability that a part is outside the specification limits.
Two-sided confidence intervals
The upper and lower bounds for the probability that a part is out-of-specification have the following formulas:
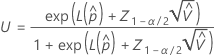
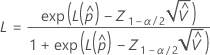
where

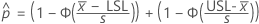
To calculate  , substitute the sample estimates for the parameters in the formula for
, substitute the sample estimates for the parameters in the formula for 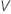 :
:



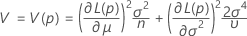
where
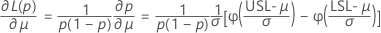

The bounds for the total PPM out-of-specification and for the total percentage out-of-specification are found by multiplying the bounds for the probability by a constant.
PPM


%
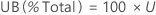

One-sided confidence bound
The upper bound for the probability a part is out-of-specification has the following formula:
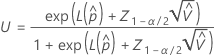
where 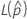 and
and  are the same as for a two-sided interval.
are the same as for a two-sided interval.
The upper bound for the total PPM out-of-specification and for the percentage out-of-specification are found by multiplying the bound for the probability by a constant.
PPM

%

Notation
| Term | Description |
|---|---|
| LSL | the lower specification limit |
| USL | the upper specification limit |
| PPM | the parts per million |
| LB | the lower bound |
| UB | the upper bound |
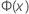 | the Cumulative Distribution Function (CDF) from a standard normal distribution |
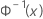 | the inverse CDF from a standard normal distribution |
 | the Probability Density Function (PDF) from a standard normal distribution |
 | the (1 - α/2)th percentile of the standard normal distribution |
| α | the alpha for the confidence level |
 | the process mean (estimated from the sample date or a historical value) |
| s | the sample standard deviation within subgroups |
| N | the total number of measurements |
| υ | the degrees of freedom for s |
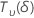 | a random variable that is distributed as a non-central t distribution with  degrees of freedom and non-centrality parameter δ degrees of freedom and non-centrality parameter δ |
Confidence intervals for PPM total for expected “within” performance for a process with one specification limit
For a process with only a Lower Specification Limit (LSL), the confidence interval for the total PPM or the total percentage out of specification is the same as the confidence interval for the PPM < LSL or % < LSL. Go to the section PPM < LSL for expected "within" performance.
For a process with only an Upper Specification Limit (USL), the confidence interval for the total PPM or the total percentage out of specification is the same as the confidence interval for the PPM > USL or % > USL. Go to the section on PPM > USL for expected "within" performance.
