A scientist for a company that manufactures processed food wants to assess the percentage of fat in the company's bottled sauce. The advertised percentage is 15%. The scientist measures the percentage of fat in 20 random samples. Previous measurements found that the population standard deviation is 2.6%.
Before collecting the data for a 1-sample Z-test, the scientist uses a power and sample size calculation to determine the sample size required to obtain a power of 0.9 and to detect a difference of 1.5% or greater.
- Choose .
- In Differences, enter 1.5.
- In Power values, enter 0.9.
- In Standard deviation, enter 2.6.
- Click OK.
Interpret the results
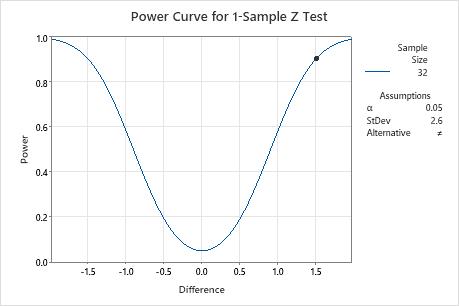
To detect a difference of 1.5% with a power of 0.9, the scientist needs to collect a sample size of 32. The scientist determines that a sample size of 32 is reasonable, and proceeds with data collection.
Results
| Difference | Sample Size | Target Power | Actual Power |
|---|---|---|---|
| 1.5 | 32 | 0.9 | 0.903816 |