In This Topic
A-Squared
The Anderson-Darling goodness-of-fit statistic (A-Squared) measures the area between the fitted line (based on the normal distribution) and the empirical distribution function (which is based on the data points). The Anderson-Darling statistic is a squared distance that is weighted more heavily in the tails of the distribution.
Interpretation
Minitab uses the Anderson-Darling statistic to calculate the p-value. The p-value is a probability that measures the evidence against the null hypothesis. A smaller p-value provides stronger evidence against the null hypothesis. A smaller value for the Anderson-Darling statistic indicates that the data follow the normal distribution more closely.
P-Value
The p-value is a probability that measures the evidence against the null hypothesis. A smaller p-value provides stronger evidence against the null hypothesis.
Interpretation
Use the p-value to determine whether the data do not follow a normal distribution.
- P-value ≤ α: The data do not follow a normal distribution (Reject H0)
- If the p-value is less than or equal to the significance level, the decision is to reject the null hypothesis and conclude that your data do not follow a normal distribution.
- P-value > α: You cannot conclude that the data do not follow a normal distribution (Fail to reject H0)
- If the p-value is larger than the significance level, the decision is to fail to reject the null hypothesis. You do not have enough evidence to conclude that your data do not follow a normal distribution.
Mean
The mean is the average of the data, which is the sum of all the observations divided by the number of observations.
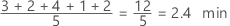
Interpretation
Use the mean to describe the sample with a single value that represents the center of the data. Many statistical analyses use the mean as a standard measure of the center of the distribution of the data.
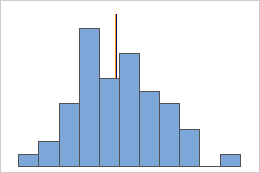
Symmetric
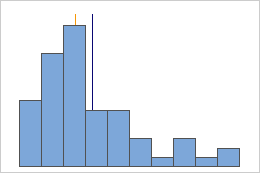
Not symmetric
For the symmetric distribution, the mean (blue line) and median (orange line) are so similar that you can't easily see both lines. But the non-symmetric distribution is skewed to the right.
StDev
The standard deviation is the most common measure of dispersion, or how spread out the data are about the mean. The symbol σ (sigma) is often used to represent the standard deviation of a population, while s is used to represent the standard deviation of a sample. Variation that is random or natural to a process is often referred to as noise.
Because the standard deviation is in the same units as the data, it is usually easier to interpret than the variance.
Interpretation
Use the standard deviation to determine how spread out the data are from the mean. A higher standard deviation value indicates greater spread in the data. A good rule of thumb for a normal distribution is that approximately 68% of the values fall within one standard deviation of the mean, 95% of the values fall within two standard deviations, and 99.7% of the values fall within three standard deviations.
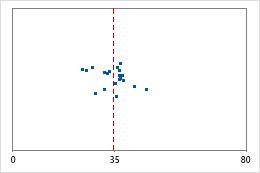
Hospital 1
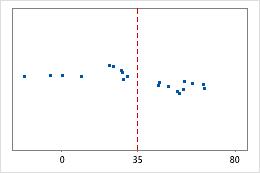
Hospital 2
Hospital discharge times
Administrators track the discharge time for patients who are treated in the emergency departments of two hospitals. Although the average discharge times are about the same (35 minutes), the standard deviations are significantly different. The standard deviation for hospital 1 is about 6. On average, a patient's discharge time deviates from the mean (dashed line) by about 6 minutes. The standard deviation for hospital 2 is about 20. On average, a patient's discharge time deviates from the mean (dashed line) by about 20 minutes.
Variance
The variance measures how spread out the data are about their mean. The variance is equal to the standard deviation squared.
Interpretation
The greater the variance, the greater the spread in the data.
Because variance (σ2) is a squared quantity, its units are also squared, which may make the variance difficult to use in practice. The standard deviation is usually easier to interpret because it's in the same units as the data. For example, a sample of waiting times at a bus stop may have a mean of 15 minutes and a variance of 9 minutes2. Because the variance is not in the same units as the data, the variance is often displayed with its square root, the standard deviation. A variance of 9 minutes2 is equivalent to a standard deviation of 3 minutes.
Skewness
Skewness is the extent to which the data are not symmetrical.
Interpretation
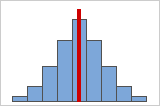
Figure A
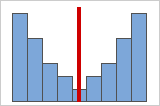
Figure B
Symmetrical or non-skewed distributions
As data becomes more symmetrical, its skewness value approaches zero. Figure A shows normally distributed data, which by definition exhibits relatively little skewness. By drawing a line down the middle of this histogram of normal data it's easy to see that the two sides mirror one another. But lack of skewness alone doesn't imply normality. Figure B shows a distribution where the two sides still mirror one another, though the data is far from normally distributed.
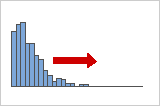
Positive or right skewed distributions
Positive skewed or right skewed data is so named because the "tail" of the distribution points to the right, and because its skewness value will be greater than 0 (or positive). Salary data is often skewed in this manner: many employees in a company make relatively little, while increasingly few people make very high salaries.
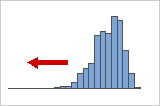
Negative or left skewed distributions
Left skewed or negative skewed data is so named because the "tail" of the distribution points to the left, and because it produces a negative skewness value. Failure rate data is often left skewed. Consider light bulbs: very few will burn out right away, the vast majority lasting for quite a long time.
Kurtosis
Kurtosis indicates how the tails of a distribution differ from the normal distribution.
Interpretation
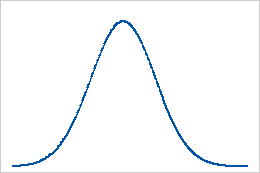
Baseline: Kurtosis value of 0
Normally distributed data establish the baseline for kurtosis. A kurtosis value of 0 indicates that the data follow the normal distribution perfectly. A kurtosis value that significantly deviates from 0 may indicate that the data are not normally distributed.
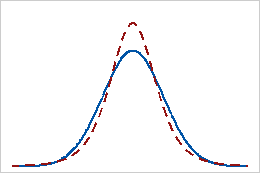
Positive kurtosis
A distribution that has a positive kurtosis value indicates that the distribution has heavier tails than the normal distribution. For example, data that follow a t-distribution have a positive kurtosis value. The solid line shows the normal distribution, and the dotted line shows a distribution that has a positive kurtosis value.
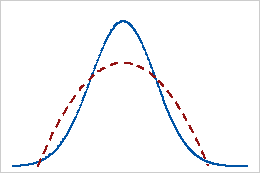
Negative kurtosis
A distribution with a negative kurtosis value indicates that the distribution has lighter tails than the normal distribution. For example, data that follow a beta distribution with first and second shape parameters equal to 2 have a negative kurtosis value. The solid line shows the normal distribution and the dotted line shows a distribution that has a negative kurtosis value.
N
The number of non-missing values in the sample.
| Total count | N | N* |
|---|---|---|
| 149 | 141 | 8 |
Minimum
The minimum is the smallest data value.
In these data, the minimum is 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Use the minimum to identify a possible outlier or a data-entry error. One of the simplest ways to assess the spread of your data is to compare the minimum and maximum. If the minimum value is very low, even when you consider the center, the spread, and the shape of the data, investigate the cause of the extreme value.
1st Quartile
Quartiles are the three values—the 1st quartile at 25% (Q1), the second quartile at 50% (Q2 or median), and the third quartile at 75% (Q3)— that divide a sample of ordered data into four equal parts.
The 1st quartile is the 25th percentile and indicates that 25% of the data are less than or equal to this value.
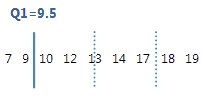
For this ordered data, the 1st quartile (Q1) is 9.5. That is, 25% of the data are less than or equal to 9.5.
Median
The median is the midpoint of the data set. This midpoint value is the point at which half the observations are above the value and half the observations are below the value. The median is determined by ranking the observations and finding the observation that are at the number [N + 1] / 2 in the ranked order. If the number of observations are even, then the median is the average value of the observations that are ranked at numbers N / 2 and [N / 2] + 1.
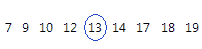
For this ordered data, the median is 13. That is, half the values are less than or equal to 13, and half the values are greater than or equal to 13. If you add another observation equal to 20, the median is 13.5, which is the average between 5th observation (13) and the 6th observation (14).
Interpretation

Symmetric

Not symmetric
For the symmetric distribution, the mean (blue line) and median (orange line) are so similar that you can't easily see both lines. But the non-symmetric distribution is skewed to the right.
3rd Quartile
Quartiles are the three values—the 1st quartile at 25% (Q1), the second quartile at 50% (Q2 or median), and the third quartile at 75% (Q3)— that divide a sample of ordered data into four equal parts.
The third quartile is the 75th percentile and indicates that 75% of the data are less than or equal to this value.
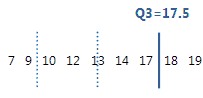
For this ordered data, the third quartile (Q3) is 17.5. That is, 75% of the data are less than or equal to 17.5.
Maximum
The maximum is the largest data value.
In these data, the maximum is 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interpretation
Use the maximum to identify a possible outlier or a data-entry error. One of the simplest ways to assess the spread of your data is to compare the minimum and maximum. If the maximum value is very high, even when you consider the center, the spread, and the shape of the data, investigate the cause of the extreme value.
Confidence Interval
The confidence interval provides a range of likely values for the population parameter. Because samples are random, two samples from a population are unlikely to yield identical confidence intervals. But, if you repeated your sample many times, a certain percentage of the resulting confidence intervals or bounds would contain the unknown population parameter. The percentage of these confidence intervals or bounds that contain the parameter is the confidence level of the interval. For example, a 95% confidence level indicates that if you take 100 random samples from the population, you could expect approximately 95 of the samples to produce intervals that contain the population parameter.
An upper bound defines a value that the population parameter is likely to be less than. A lower bound defines a value that the population parameter is likely to be greater than.
The confidence interval helps you assess the practical significance of your results. Use your specialized knowledge to determine whether the confidence interval includes values that have practical significance for your situation. If the interval is too wide to be useful, consider increasing your sample size. For more information, go to Ways to get a more precise confidence interval.
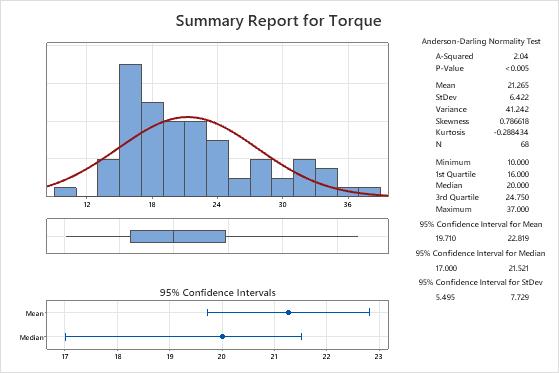
- The population mean for the torque measurements is between 19.710 and 22.819.
- The population median for the torque measurements is between 17 and 21.521.
- The population standard deviation for the torque measurements is between 5.495 and 7.729.
Histogram
A histogram divides sample values into many intervals and represents the frequency of data values in each interval with a bar.
Interpretation
Use a histogram to assess the shape and spread of the data. Histograms are best when the sample size is greater than 20.
- Skewed data
-
You can use a histogram of the data overlaid with a normal curve to examine the normality of your data. A normal distribution is symmetric and bell-shaped, as indicated by the curve. It is often difficult to evaluate normality with small samples. A probability plot is best for determining the distribution fit.
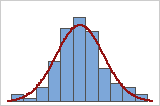
Good fit
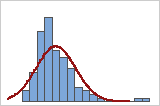
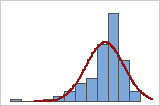
Poor fit
- Outliers
-
Outliers, which are data values that are far away from other data values, can strongly affect the results of your analysis. Often, outliers are easiest to identify on a boxplot.
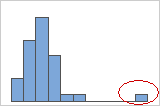
On a histogram, isolated bars at either ends of the graph identify possible outliers.
Try to identify the cause of any outliers. Correct any data–entry errors or measurement errors. Consider removing data values for abnormal, one-time events (also called special causes). Then, repeat the analysis. For more information, go to Identifying outliers.
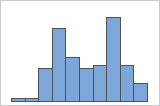
- Multi-modal data
-
Multi-modal data have multiple peaks, also called modes. Multi-modal data often indicate that important variables are not yet accounted for.
Simple
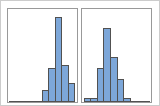
With Groups
For example, a manager at a bank collects wait time data and creates a simple histogram. The histogram appears to have two peaks. After further investigation, the manager determines that the wait times for customers who are cashing checks is shorter than the wait time for customers who are applying for home equity loans. The manager adds a group variable for customer task, and then creates a histogram with groups.
If you have additional information that allows you to classify the observations into groups, you can create a group variable with this information. Then, you can create the graph with groups to determine whether the group variable accounts for the peaks in the data.
Boxplot
A boxplot provides a graphical summary of the distribution of a sample. The boxplot shows the shape, central tendency, and variability of the data.
Interpretation
Use a boxplot to examine the spread of the data and to identify any potential outliers. Boxplots are best when the sample size is greater than 20.
- Skewed data
-
Examine the spread of your data to determine whether your data appear to be skewed. When data are skewed, the majority of the data are located on the high or low side of the graph. Often, skewness is easiest to detect with a histogram or boxplot.
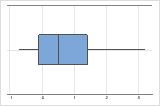
Right-skewed
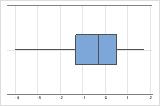
Left-skewed
The boxplot with right-skewed data shows wait times. Most of the wait times are relatively short, and only a few wait times are long. The boxplot with left-skewed data shows failure time data. A few items fail immediately, and many more items fail later.
- Outliers
-
Outliers, which are data values that are far away from other data values, can strongly affect the results of your analysis. Often, outliers are easiest to identify on a boxplot.
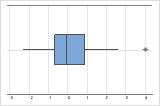
On a boxplot, asterisks (*) denote outliers.
Try to identify the cause of any outliers. Correct any data–entry errors or measurement errors. Consider removing data values for abnormal, one-time events (also called special causes). Then, repeat the analysis. For more information, go to Identifying outliers.
